Así explican las matemáticas cómo funciona nuestro cerebro

10 AGO 2016 - 08:59 ART

Esquema de las células que forman parte de la retina, por Ramón y Cajal.

Interpretamos el mundo a través de nuestros sentidos, o eso creíamos: los nervios ópticos o sus equivalentes para otros sentidos transmitían la información exterior e interior a nuestro cerebro y allí se interpretaban. Lo que la investigación ha revelado en los últimos años es que nuestro cerebro es mucho más complejo, y que durante nuestra vida va adquiriendo experiencia y construyendo una enorme biblioteca a la que acude cuando recibimos algún estímulo para identificarlo, ponerlo en contexto y tomar las decisiones de comportamiento más adecuadas en cada momento. Comprender cómo funciona todo este proceso precisa de las matemáticas y describiremos a continuación cómo diversas ramas de esta disciplina intervienen en esta tarea. Debemos decir que las matemáticas no van solas y que las técnicas computacionales juegan también un papel clave.

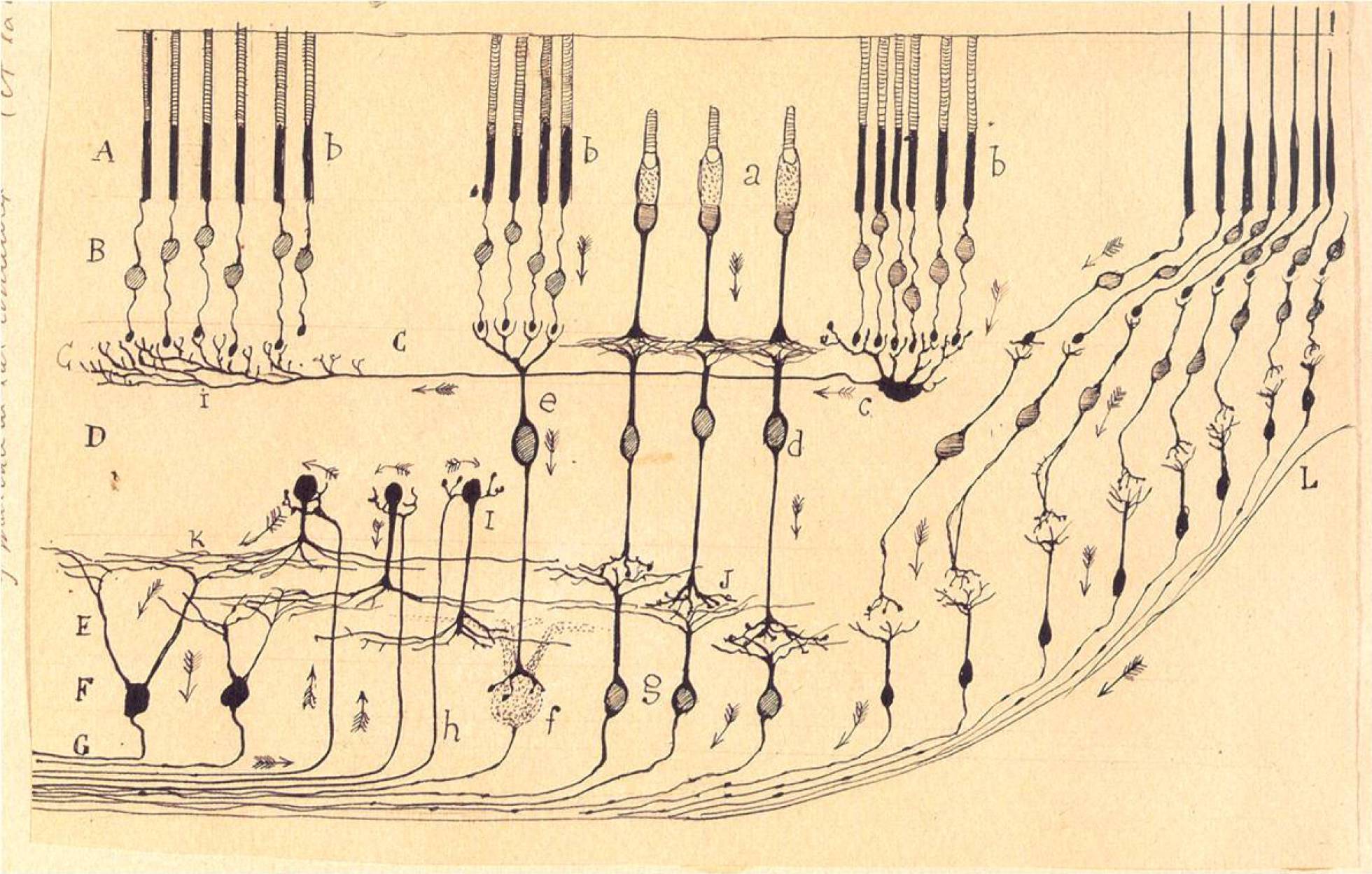
Desde que Santiago Ramón y Cajal describiera las neuronas y las sinapsis entre ellas, está claro que el sistema nervioso es una gran red, cuyos nodos son las neuronas y cuyas aristas son las sinapsis

Una rama de las matemáticas que tiene una obvia implicación en el entendimiento de las redes neuronales es la teoría de grafos. Desde que Santiago Ramón y Cajal describiera las neuronas y las sinapsis entre ellas, está claro que el sistema nervioso es una gran red, cuyos nodos son las neuronas y cuyas aristas son las sinapsis. Es un modelo simplificado ya que las conexiones son múltiples, algunas bidireccionales y otras no, pero ya sirve para que podamos poner en marcha toda la potencia de la teoría de grafos y extraer conclusiones. Por ejemplo, es posible determinar la estructura global de la red a partir de estudios de imagen cerebral no invasiva; esta estrategia permite determinar la relevancia que los distintos nodos o estructuras cerebrales tienen para distintos comportamientos y, finalmente, predecir cómo cambiará éste si se producen daños, aun mínimos, en cualquier parte del cerebro. Lo verdaderamente interesante es que, en un futuro no lejano, se podrá actuar sobre alguno de estos nodos cerebrales específicamente para paliar los efectos derivados de muchas enfermedades neurológicas.

También se utilizan métodos de dinámica no lineal. Ya desde los pioneros modelos en dimensiones uno y dos desarrollados por Hodgkin y Huxley, los sistemas dinámicos no lineales se situaron en el corazón de la investigación en neurociencia. No debemos olvidar que el cerebro es un sistema dinámico, y es necesario entender cómo se comunican las neuronas, si ante un suceso determinado producen potenciales de acción, que forman la base de su lenguaje, o no; y si lo hacen, cuál es su ritmo. Todo ello nos dirá finalmente cómo funciona nuestro pensamiento y cómo este se adapta, aprende y madura. Este conocimiento será fundamental para abordar muchos problemas con una gran relevancia social, como la educación o incluso las peculiaridades de nuestro marco legal y ético.

Otra área fundamental es la teoría de probabilidades y la estadística. Si nuestro cerebro crea una biblioteca, ¿cuál es la probabilidad de que ante un estímulo concreto encuentre el “libro” adecuado? Los métodos bayesianos son aquí la clave.

En conclusión, nuestras neuronas son mejores matemáticas de lo que pensamos, y si de acuerdo con Galileo el mundo exterior se describe con lenguaje matemático así deberá ser también nuestro mundo interior; en caso contrario, no seríamos capaces de comprenderlo.

Manuel de León (Instituto de Ciencias Matemáticas) y Luis M. Martínez (Instituto de Neurociencias) son investigadores del CSIC. Ambos son también codirectores de los CorBI International Courses,un programa de formación de excelencia en biomedicina. En su primera edición reunió a jóvenes investigadores y científicos de primera línea internacional en A Coruña, del 26 de julio al 5 de agosto de 2016.