
Matemáticas para explicar las medidas contra el coronavirus
Partiendo de un número bajo de infectados con el nuevo coronavirus, en poco tiempo puede haber una gran cantidad de personas contagiadas que no pueda asimilar el sistema sanitario. Así lo reflejan las curvas matemáticas de crecimiento exponencial, una realidad que va aceptando la población y que ha obligado al Gobierno de España a adoptar medidas extraordinarias para contener la pandemia.
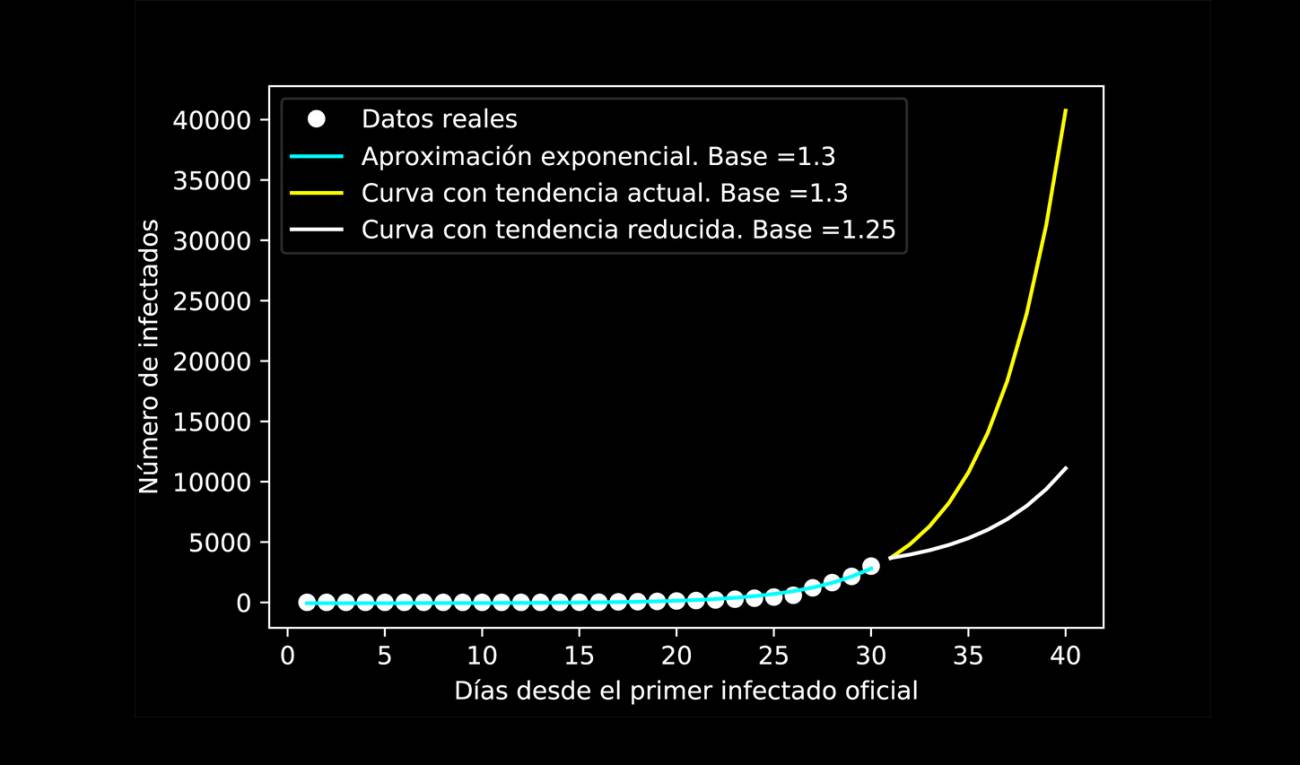
Curva de crecimiento exponencial de la infección con datos reales (a fecha 12 de marzo de 2020) facilitados por el Gobierno de España, y predicción de crecimiento con la tendencia actual sin medidas (línea amarilla) y con el efecto probable de las medidas tomadas por las autoridades (línea blanca). / A. Galisteo/ IMDEA Networks
El propósito de las medidas que están tomando las autoridades es frenar la expansión del virus. Para entender esas medidas es imprescindible saber cómo funciona la propagación. Supongamos que somos el paciente cero de una enfermedad como esta. Los contagios que provoquemos dependerán de dos factores.
Por un lado, del número de personas con las que interactuemos. Si fuéramos un ermitaño en mitad del bosque que no se relaciona con nadie, en cuanto nos curásemos o muriésemos de la enfermedad, ésta ya no se propagaría más.
Por otro lado, está la forma en la que se transmite la enfermedad. Algunas enfermedades, como el ébola, son más difíciles de contagiar porque se transmiten en gotas gordas, lo que requiere mucha cercanía con el enfermo. Otras, como la tuberculosis, tienen un factor de propagación más alto ya que la bacteria se aloja en las gotas más pequeñas. El coronavirus se trasmite en gotas medias, lo que implica que a partir de cierta distancia de la persona infectada, caen al suelo y no llegan a la gente de su alrededor.
Para saber cómo crece ese contagio se usan las matemáticas. Si queremos conocer el número de contagiados que habrá mañana debemos partir del número de infectados que hay hoy. Hay que tener en cuenta el número de personas con las que esos infectados han interactuado hoy, hallar la probabilidad media de contagio y multiplicar los dos números.
Por último, al resultado hay que restarle los que se han curado. Como la enfermedad es relativamente larga, por ahora el número de pacientes curados es mucho menor que el de los que se infectan cada día, aunque con una gran probabilidad se vayan a curar en el futuro.
Este modelo de contagio es exponencial. Esto significa que no sólo la enfermedad contagia cada día a más gente, sino que la velocidad de contagio también aumenta. Supongamos que de media cada infectado contagia a una persona al día. El segundo día habrá dos contagiados, el tercero cuatro, a la semana 128 y a los veinte días más de un millón de personas.
Esta propiedad es precisamente la que es tan asombrosa y terrible de los comportamientos exponenciales: crecen muy rápido partiendo de números relativamente bajos.
Los organismos públicos que están tomando medidas a escala europea, nacional, regional y municipal trabajan con modelos capaces de predecir de manera aproximada cuántos casos puede haber en una zona determinada y cómo va a extenderse la epidemia.
El número de contagios medios por paciente y día varía de región a región. La razón de esa diferencia es que hay muchos factores implicados: la cultura del país, por ejemplo si acostumbramos a una mayor cercanía corporal como en los países mediterráneos o una separación mayor como en los nórdicos; la humedad del ambiente, ya que con más humedad las gotas en las que se propaga el virus viajan a menor distancia; el número de personas con las que estamos en contacto a diario, por ejemplo si la mayoría vive en grandes aglomeraciones o en pequeñas poblaciones, etc…
Como toda enfermedad, llegará un momento en el que se estabilizará. Esto puede pasar porque se tomen las medidas adecuadas y el número de pacientes no se incremente, porque se cree una vacuna que ayude a detenerla o porque la mayoría de la población haya estado expuesta y se haya inmunizado.
Los sistemas sanitarios tienen una capacidad limitada
La pregunta que está en la mente de muchos es: ¿por qué los gobiernos están tomando medidas tan drásticas si al final sea como sea se va a estabilizar? Se debe a que lo importante no es cuándo se estabilice la pandemia, sino a cuánta gente haya afectado cuando lo haga ya que los sistemas sanitarios tienen una capacidad limitada.
Si todos enfermamos a la vez, el sistema no podrá atendernos. Esto es lo que están tratando de impedir los gobiernos. Y para ello tratan de controlar las variables que intervienen en el crecimiento exponencial.
La primera es el número de interacciones que tenemos con otras personas, al que llamamos R. Si nos damos una vuelta por una zona poco poblada, R será cercano a 0. Pero si vamos a un partido de fútbol o estamos en un aula del colegio el valor de R aumenta mucho.
Los gobiernos están fomentando el teletrabajo, cerrando clases, aplazando reuniones y cancelando cualquier actividad en la que participen muchas personas para que las interacciones sean lo más bajas posible. Y aquí además interviene otro factor del Covid-19, y es que una gran parte de los infectados son asintomáticos o con pocos síntomas. Esto hace que haya mucha gente infectada que no lo sabe, pero su comportamiento es clave para no extender la pandemia.
Por otro lado, no todas las personas que entren en nuestro ‘radio de contaminación’ nos infectarán, sino que existe una probabilidad de que lo hagan, p. Si estamos en una fiesta y hablamos muy cerca de otras personas, tocamos muchas superficies y luego nos llevamos las manos a la cara sin lavarnos, por ejemplo, las probabilidades de contagiarnos son mucho mayores.
Por ello se están creando campañas de concienciación, suministrando productos de higiene de manos en sitios públicos en forma de geles y pidiéndonos que no nos toquemos la cara con las manos. Para saber lo efectivas que son estas medidas hay que entender que precisamente porque tiene un incremento exponencial, reducir cada centésima posible en la base tiene un impacto tremendo a lo largo del tiempo.
Ander Galisteo es investigador del Instituto IMDEA Networks y la Universidad Carlos III de Madrid (UC3M)
Fuente:
SINC
Derechos: Creative Commons.
































No hay comentarios:
Publicar un comentario