28th Annual Computational Neuroscience Meeting: CNS*2019 | BMC Neuroscience | Full Text

28th Annual Computational Neuroscience Meeting: CNS*2019 | BMC Neuroscience | Full Text

P81 Information transmission in delay-coupled neuronal circuits

Jaime Sánchez Claros1, Claudio Mirasso1, Minseok Kang2, Aref Pariz1, Ingo Fischer1

1Institute for Cross-Disciplinary Physics and Complex Systems, Palma de Mallorca, Spain; 2Institute for Cross-Disciplinary Physics and Complex Systems, Osnabrck University, Osnabrck, Germany

Correspondence: Jaime Sánchez Claros (js.claros27@gmail.com)

BMC Neuroscience 2019, 20(Suppl 1):P81

The information that we receive through our sensory system (e.g. sound, vision, pain, etc), needs to be transmitted to different regions of the brain for its processing. When these regions are sufficiently separated from each other, the latency in the communication can affect the synchronization state; it is possible that the regions synchronize in phase or out of phase, or even not synchronize [1]. These types of synchronization, when occur, can have important consequences in information transmission and processing [2].

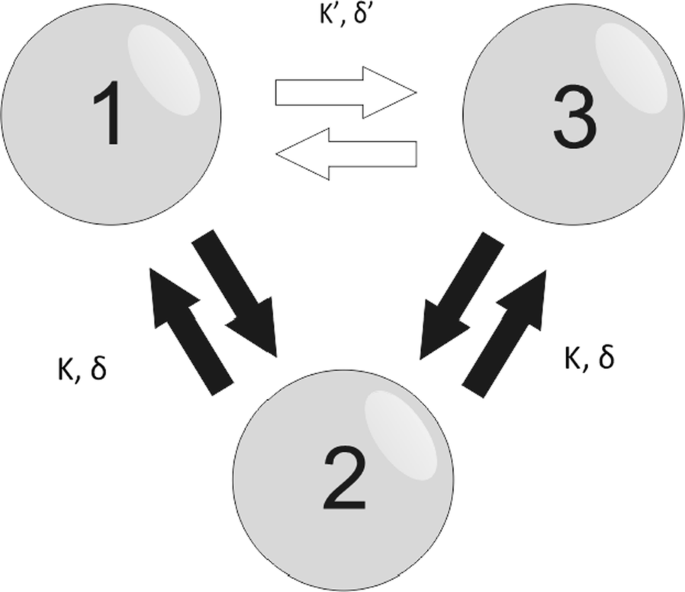
Here we study the information transmission in a V and a circular motif (see Fig. 1). We initially use the Kuramoto model to describe the nodes dynamics and derive analytical stability solutions for the V-motif for different delays and coupling strengths among the neurons as well as different spiking frequencies. We then analyze the effect that a third connection would have on the stable solutions as we change its axonal delay and synaptic strength. For a more realistic model, we simulate the Hodgkin-Huxley neuron model. For the V-motif we find that the delay can play an important role in the efficiency of the signal transmission. When we introduce a direct connection between 1 and 3, we find changes in the stability conditions and so the efficacy of the information transmission. To distinguish between rate and temporal coding, we modulate one of the elements with low and high frequency signals, respectively, and investigate the signal transmission to the other neurons using delayed mutual information and delayed transfer entropy [3].

Fig. 1

Three bidirectionally connected neurons. Two outer nodes (1 and 3) are bidirectionally connected to a middle node (2) with the same synaptic strength K and delay δ thus creating the V-motif. The addition of third bidirectional connection (white arrows) with synaptic strength K’ and delay δ’ between two outer nodes gives rise to the circular motif

Full size image

References

1. 1.
   Sadeghi S, Valizadeh A. Synchronization of delayed coupled neurons in presence of inhomogeneity. Journal of Computational Neuroscience 2014, 36, 55–66.
2. 2.
   Mirasso CR, Carelli PV, Pereira T, Matias FS, Copelli M. Anticipated and zero-lag synchronization in motifs of delay-coupled systems. Chaos 2017, 27,114305.
3. 3.
   Kirst C, Timme M, Battaglia D. Dynamic information routing in complex networks. Nature communication 2016, 7.

P82 A Liquid State Machine pruning method for identifying task specific circuits

Dorian Florescu

Coventry University, Coventry, United Kingdom

Correspondence: Dorian Florescu (dorian.florescu@coventry.ac.uk)

BMC Neuroscience 2019, 20(Suppl 1):P82

The current lack of knowledge on the precise neural circuits responsible for performing sensory and motor tasks, despite the large amounts of neuroscience data available, significantly slows down the development of new treatments for impairments caused by neurodegenerative diseases.

The Liquid State Machine (LSM) is one of the widely used paradigms for modelling brain computation. This model consists of a fixed recurrent spiking neural network, called Liquid, and a linear Readout unit with adjustable synapses. The model possesses, under idealised conditions, universal real-time computing power [1]. It was shown that, when the connections in the Liquid are modelled as dynamical synapses, this model can reproduce accurately the behaviour of the rat cortical microcircuits [1]. However, it is still largely unknown which neurons and synapses in the Liquid play a key role in a task performed by the LSM. Several proposed methods train the Liquid in addition to the Readout [2], which leads to improvements in accuracy and network sparsity, but offers little insight into the functioning of the original Liquid.

In the typical LSM architecture, the spike trains generated by the Liquid neurons are filtered before being processed by the Readout. It was shown that using the exact spike times generated by the Liquid neurons, rather than the filtered spike times, results in a much better performance of LSMs on training tasks. The algorithm introduced, called the Orthogonal Forward Regression with Spike Times (OFRST), leads to higher accuracy and fewer Readout connections than the state-of-the-art algorithm [3].

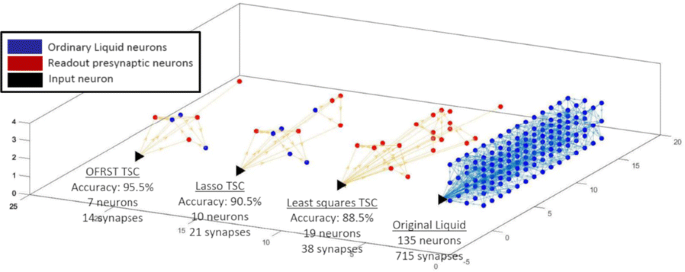
This work proposes an analysis of the underlying mechanisms used by the LSM to perform a computational task by searching for the key neural circuits involved. Given an LSM trained on a classification task, a new algorithm is introduced that identifies the corresponding task specific circuit (TSC), defined as the set of neurons and synapses in the Liquid that have a contribution to the Readout output. Thorough numerical simulations, I show that the TSC computed with the proposed algorithm has fewer neurons and higher performance when the training is done with OFRST compared with other state-of-the-art training methods (Fig. 1).

Fig. 1

The task specific circuits (TSCs), computed with the proposed algorithm, corresponding to the classification task of discriminating jittered spike trains belonging to two classes. The training is done with three methods: OFRST, Least Squares, and Lasso. OFRST, the only method processing exact spike times, leads to the smallest circuit and the best performance on the validation dataset

Full size image

I introduce a new representation for the Liquid dynamical synapses, which demonstrates that they can be mapped onto operators on the Hilbert space of spike trains. Based on this representation, I develop a novel algorithm that removes iteratively the synapses of a TSC based on the exact spike times generated by the Liquid neurons. Additional numerical simulations show that the proposed algorithm improves the LSM classification performance and leads to a significantly sparser representation. For the same initial Liquid, but different tasks, the proposed algorithm results in different TSCs that, in some cases, have no neurons in common. These results can lead to new methods to synthesize Liquids by interconnecting dedicated neural circuits.

References

1. 1.
   Maass W, Natschläger T, Markram H. Computational models for generic cortical microcircuits. Computational neuroscience: A comprehensive approach 2004;18:575–605.
2. 2.
   Yin J, Meng Y, Jin Y. A developmental approach to structural self-organization in reservoir computing. IEEE transactions on autonomous mental development 2012 Dec;4(4):273–89.
3. 3.
   Florescu D, Coca D. Learning with precise spike times: A new approach to select task-specific neurons. In Computational and Systems Neuroscience (COSYNE) 2018 Mar 2. COSYNE.

P83 Cross-frequency coupling along the soma-apical dendritic axis of model pyramidal neurons

Melvin Felton1, Alfred Yu2, David Boothe2, Kelvin Oie2, Piotr Franaszczuk2

1U.S. Army Research Laboratory, Computational and Information Sciences Division, Adelphi, MD, United States of America; 2U.S. Army Research Laboratory, Human Research and Engineering Directorate, Aberdeen Proving Ground, MD, United States of America

Correspondence: Piotr Franaszczuk (pfranasz@gmail.com)

BMC Neuroscience 2019, 20(Suppl 1):P83

Cross-frequency coupling (CFC) has been associated with mental processes like perceptual and memory-related tasks, and is often observed via EEG and LFP measurements [1]. There are a variety of physiological mechanisms believed to produce CFC, and different types of network properties can yield distinct CFC signatures [2]. While it is widely believed that pyramidal neurons play an important role in the occurrence of CFC, the detailed nature of the contribution of individual pyramidal neurons to CFC detected via large-scale measures of brain activity is still uncertain.

As an extension of our single model neuron resonance analysis [3], we examined CFC along the soma-apical dendrite axis of realistic models of pyramidal neurons. We configured three models to capture some variety that exists among pyramidal neurons in the neocortical and limbic regions of the brain. Our baseline model had the least amount of regional variation in conductance densities of the Ih and high- and low-threshold Ca2+ conductances. The second model had an exponential gradient in Ih conductance density along the soma-apical dendrite axis, typical of some neocortical and hippocampal pyramidal neurons. The third model contained both the exponential gradient in Ih conductance density and a distal apical “hot zone” where the high- and low-threshold Ca2+conductances had densities 10 and 100 times higher, respectively, than anywhere else in the model (cf., [3]). We simulated two current injection scenarios: 1) perisomatic 4 Hz modulation with perisomatic, mid-apical, and distal apical 40 Hz injections; and 2) distal 4 Hz modulation with perisomatic, mid-apical, and distal 40 Hz injections. We used two metrics to quantify the strength of CFC—height ratio and modulation index [4].

We found that CFC strength can be predicted from the passive filtering properties of the model neuron. Generally, regions of the model with much larger membrane potential fluctuations at 4 Hz than at 40 Hz (high Vm4Hz/Vm40Hz) had stronger CFC. The strongest CFC values were observed in the baseline model, but when the exponential gradient in Ih conductance density was added, CFC strength decreased by almost 50% at times. On the other hand, including the distal hot zone increased CFC strength slightly above the case with only the exponential gradient in Ih conductance density.

This study can potentially shed light on which configurations of fast and slow input to pyramidal neurons can produce the strongest CFC, and where exactly within the neuron CFC is strongest. In addition, this study can illuminate the reasons why there may be differences between CFC strength observed in different regions of the brain and between different populations of neurons.

References

1. 1.
   Tort AB, Komorowski RW, Manns JR, Kopell NJ, Eichenbaum H. Theta–gamma coupling increases during the learning of item–context associations. Proceedings of the National Academy of Sciences 2009 Dec 8;106(49):20942–7.
2. 2.
   Hyafil A, Giraud AL, Fontolan L, Gutkin B. Neural cross-frequency coupling: connecting architectures, mechanisms, and functions. Trends in neurosciences 2015 Nov 1;38(11):725–40.
3. 3.
   Felton Jr MA, Alfred BY, Boothe DL, Oie KS, Franaszczuk PJ. Resonance Analysis as a Tool for Characterizing Functional Division of Layer 5 Pyramidal Neurons. Frontiers in Computational Neuroscience 2018;12.
4. 4.
   Tort AB, Komorowski R, Eichenbaum H, Kopell N. Measuring phase-amplitude coupling between neuronal oscillations of different frequencies. Journal of neurophysiology 2010 May 12;104(2):1195–210.

P84 Regional connectivity increases low frequency power and heterogeneity

David Boothe, Alfred Yu, Kelvin Oie, Piotr Franaszczuk

U.S. Army Research Laboratory, Human Research and Engineering Directorate, Aberdeen Proving Ground, MD, United States of America

Correspondence: David Boothe (david.l.boothe7.civ@mail.mil)

BMC Neuroscience 2019, 20(Suppl 1):P84

The relationship between neuronal connectivity and frequency in the power spectrum of calculated local field potentials is poorly characterized in models of cerebral cortex. Here we present a simulation of cerebral cortex based on the Traub model [1] implemented in the GENESIS neuronal simulation environment. We found that this model tended to produce high neuronal firing rates and strongly rhythmic activity in response to increases in neuronal connectivity. In order to simulate spontaneous brain activity with a 1/f power spectrum as observed using electroencephalogram (EEG) (cf. [2]), and to faithfully recreate the sparse nature of cortical neuronal activity we re-tuned the original Traub parameters to eliminate intrinsic neuronal activity and removed the gap junctions. While gap junctions are known to exist in adult human cortex, their exact functional role in generating spontaneous brain activity is at present poorly characterized. Tuning out intrinsic neuronal activity allows changes to the synaptic connectivity to be central to changing overall model activity.

The model we present here consists of 16 simulated cortical regions each containing 976 neurons (15,616 neurons total). Simulated cortical regions are connected via short association fibers between adjacent cortical regions originating from pyramidal cells in cortical layer 2/3 (P23s). In the biological brain these short association fibers connect local cortical regions that tend to share a function like the myriad of visual areas of the posterior, parietal and temporal cortices [4]. Because of their ubiquity across cortex short association fibers were a natural starting point for our simulations. Long range layer 2/3 pyramidal cell connections terminated on neurons in other cortical regions with the same connectivity probabilities that they have locally within a region. We then varied the relative levels of long range and short-range connectivity and observed the impact on overall model activity. Because model dynamics were very sensitive to the overall number of connections we had to be careful that the simulations we were comparing only varied in proportion of long and short range connections and not in terms of total connectivity.

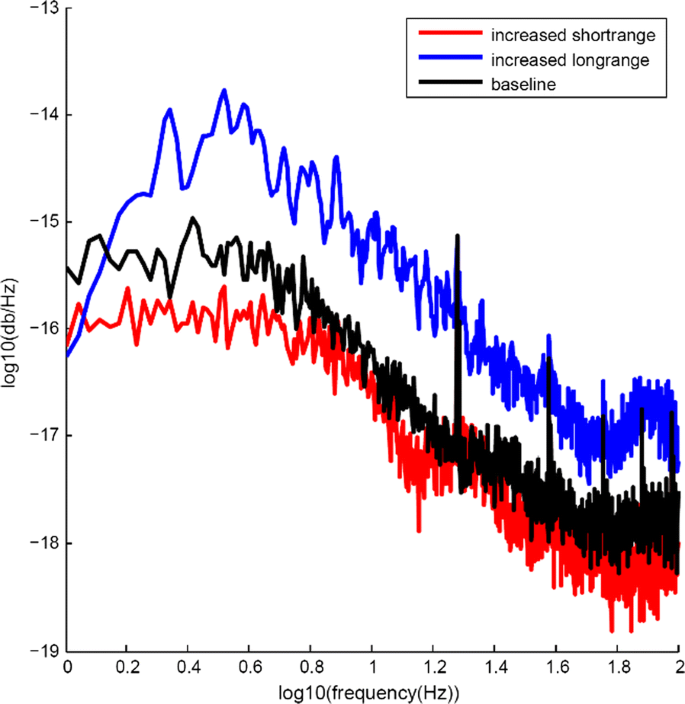
Our starting point for these simulations was a model with relatively sparse connectivity, which exhibited 1/f power spectrum with strong peaks in power spectral density at 20 Hz and 40 Hz ((Fig. 1), black line). We found that increases in long range connectivity increased power across the entire 1 to 100 Hz range of the overall local field potential of the model ((Fig. 1), blue line) and also increased heterogeneity in the power spectra of the 16 individual cortical regions. Increasing short range connectivity had the opposite effect, with overall power in the low frequency range (1 to 10 Hz) being reduced while the relative intensity at 20 Hz and 40 Hz remained constant (Fig. 1, red line). We will explore how consistent this effect is across varying levels of short- and long-range connectivity and model configuration.

Fig. 1

Differential impact of changes to short- and long-range connectivity. Black line shows power spectrum of model LFP. Blue line shows increase in LFP power across 1 to 100 Hz frequency range when long range connectivity is increased. Red line shows reduction in model power in 1 to 10 Hz range due to increase in short range connectivity

Full size image

References

1. 1.
   Traub RD, Contreras D, Cunningham MO, et al. Single-column thalamocortical network model exhibiting gamma oscillations, sleep spindles, and epileptogenic bursts. Journal of neurophysiology 2005 Apr;93(4):2194–232.
2. 2.
   Le Van Quyen M. Disentangling the dynamic core: a research program for a neurodynamics at the large-scale. Biological research 2003;36(1):67–88.
3. 3.
   Salin PA, Bullier J. Corticocortical connections in the visual system: structure and function. Physiological reviews 1995 Jan 1;75(1):107–54.

P85 Cortical folding modulates the effect of external electrical fields on neuronal function

Alfred Yu, David Boothe, Kelvin Oie, Piotr Franaszczuk

U.S. Army Research Laboratory, Human Research and Engineering Directorate, Aberdeen Proving Ground, MD, United States of America

Correspondence: David Boothe (david.l.boothe7.civ@mail.mil)

BMC Neuroscience 2019, 20(Suppl 1):P85

Transcranial electrical stimulation produces an electrical field that propagates through cortical tissue. Finite element modeling has shown that individual variation in spatial morphology can lead to variability in field strength within target structures across individuals [1]. Using GENESIS, we simulated a 10x10 mm network of neurons with spatial arrangements simulating microcolumns of a single cortical region spread across sulci and gyri. We modeled a transient electrical field with distance-dependent effects on membrane polarization, simulating the nonstationary effects of electrical fields on neuronal activity at the compartment level. In previous work, we have modeled applied electrical fields using distant electrodes, resulting in uniform orientation and field strength across all compartments. In this work, we examine a more realistic situation with distance- and orientation-dependent drop-off in field strength. As expected, this change resulted in a greater degree of functional variability between microcolumns and reduced overall network synchrony. We show that the spatial arrangement of cells within sulci and gyri yields sub-populations that are differentially susceptible to externally applied electric fields, in both their firing rates and the functional connectivity with adjacent microcolumns. In particular, pyramidal cell populations with inconsistently oriented apical dendrites produce less synchronized activity within an applied external field. Further, we find differences across cell types, such that cells with reduced dendritic arborization had greater sensitivity to orientation changes due to placement within sulci and gyri. Given that there is individual variability in the spatial arrangement of even primary cortices [2], our findings indicate that individual differences in outcomes of neurostimulation can be the result of variations in local topography. In summary, aside from increasing cortical surface area and altering axonal connection distances, cortical folding may additionally shape the effects of spatially local influences such as electrical fields.

References

1. 1.
   Datta A. Inter-individual variation during transcranial direct current stimulation and normalization of dose using MRI-derived computational models. Frontiers in psychiatry 2012 Oct 22;3:91.
2. 2.
   Rademacher J, Caviness Jr VS, Steinmetz H, Galaburda AM. Topographical variation of the human primary cortices: implications for neuroimaging, brain mapping, and neurobiology. Cerebral Cortex 1993 Jul 1;3(4):313–29.

P86 Data-driven modeling of mouse CA1 and DG neurons

Paola Vitale1, Carmen Alina Lupascu1, Luca Leonardo Bologna1, Mala Shah2, Armando Romani3, Jean-Denis Courcol3, Stefano Antonel3, Werner Alfons Hilda Van Geit3, Ying Shi3, Julian Martin Leslie Budd4, Attila Gulyas4, Szabolcs Kali4, Michele Migliore1, Rosanna Migliore1, Maurizio Pezzoli5, Sara Sáray6, Luca Tar6, Daniel Schlingloff7, Peter Berki4, Tamas F. Freund4

1Institute of Biophysics, National Research Council, Palermo, Italy; 2UCL School of Pharmacy, University College London, School of Pharmacy, London, United Kingdom; 3École Polytechnique Fédérale de Lausanne, Blue Brain Project, Lausanne, Switzerland; 4Institute of Experimental Medicine, Hungarian Academy of Sciences, Budapest, Hungary; 5Laboratory of Neural Microcircuitry (LNMC),Brain Mind Institute, EPFL, Lausanne, Switzerland; 6Hungarian Academy of Sciences and Pázmány Péter Catholic University, Institute of Experimental Medicine and Information Technology and Bionics, Budapest, Hungary; 7Hungarian Academy of Sciences and Semmelweis University, Institute of Experimental Medicine and János Szentágothai Doctoral School of Neurosciences, Budapest, Hungary

Correspondence: Paola Vitale (paola.vitale@pa.ibf.cnr.it)

BMC Neuroscience 2019, 20(Suppl 1):P86

Implementing morphologically and biophysically accurate single cell models, capturing the electrophysiological variability observed experimentally, is the first crucial step to obtain the building blocks to construct a brain region at the cellular level.

We have previously applied a unified workflow to implement a set of optimized models of CA1 neurons and interneurons of rats [1]. In this work, we apply the same workflow to implement detailed single cell models of CA1 and DG mouse neurons. An initial set of kinetic models and dendritic distributions of the different ion channels present on each type of cells studied neurons was defined, consistently with the available experimental data. Many electrophysiological features were then extracted from a set of experimental traces obtained under somatic current injections. For this purpose, we used the eFEL tool available on the Brain Simulation Platform of the HBP (https://collab.humanbrainproject.eu/#/collab/1655/nav/66850). Interestingly, for both cell types we observed rather different firing patterns within the same cell population, suggesting that a given population of cells in the mouse hippocampus cannot be considered as belonging to a single firing type. For this reason, we have chosen to cluster the experimental traces on the basis of the number of spikes as a function of the current injection and optimize each group independently from the others. We identified four different types of firing behavior for both DG’s granule cells and CA1’s pyramidal neurons. To create the optimized models, we used the BluePyOpt Optimization library [2] with several different accurate morphologies. Simulations were run on HPC systems at Cineca, Jülich, and CSCS. The results of the models for CA1 and DG will be discussed also in comparison with the models obtained for the rat.

References

1. 1.
   Migliore R, Lupascu CA, Bologna LL, et al. The physiological variability of channel density in hippocampal CA1 pyramidal cells and interneurons explored using a unified data-driven modeling workflow. PLoS computational biology 2018 Sep 17;14(9):e1006423.
2. 2.
   Van Geit W, Gevaert M, Chindemi G, et al. BluePyOpt: leveraging open source software and cloud infrastructure to optimize model parameters in neuroscience. Frontiers in neuroinformatics 2016 Jun 7;10:17.

P87 Memory compression in the hippocampus leads to the emergence of place cells

Marcus K. Benna, Stefano Fusi

Columbia University, Center for Theoretical Neuroscience, Zuckerman Mind Brain Behavior Institute, New York, NY, United States of America

Correspondence: Marcus K. Benna (mkb2162@columbia.edu)

BMC Neuroscience 2019, 20(Suppl 1):P87

The observation of place cells in the hippocampus has suggested that this brain area plays a special role in encoding spatial information. However, several studies show that place cells do not only encode position in physical space, but that their activity is in fact modulated by several other variables, which include the behavior of the animal (e.g. speed of movement or head direction), the presence of objects at particular locations, their value, and interactions with other animals. Consistent with these observations, place cell responses are reported to be rather unstable, indicating that they encode multiple variables, many of which are not under control in experiments, and that the neural representations in the hippocampus may be continuously updated. Here we propose a memory model of the hippocampus that provides a novel interpretation of place cells and can explain these observations. We hypothesize that the hippocampus is a memory device that takes advantage of the correlations between sensory experiences to generate compressed representations of the episodes that are stored in memory. We have constructed a simple neural network model that can efficiently compress simulated memories. This model naturally produces place cells that are similar to those observed in experiments. It predicts that the activity of these cells is variable and that the fluctuations of the place fields encode information about the recent history of sensory experiences. Our model also suggests that the hippocampus is not explicitly designed to deal with physical space, but can equally well represent any variable with which its inputs correlate. Place cells may simply be a consequence of a memory compression process implemented in the hippocampus.

P88 The information decomposition and the information delta: A unified approach to disentangling non-pairwise information

James Kunert-Graf, Nikita Sakhanenko, David Galas

Pacific Northwest Research Institute, Galas Lab, Seattle, WA, United States of America

Correspondence: James Kunert-Graf (kunert@uw.edu)

BMC Neuroscience 2019, 20(Suppl 1):P88

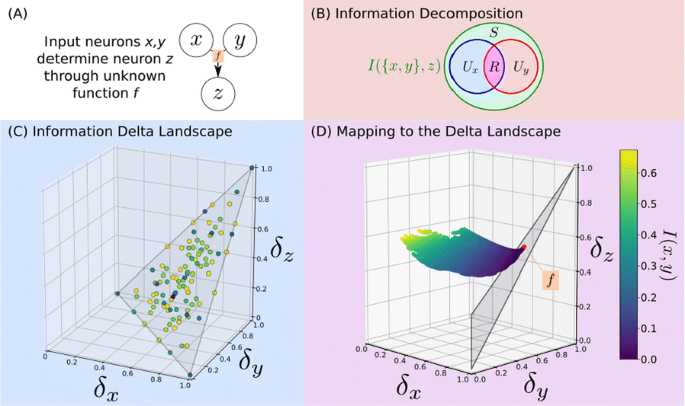
Neurons in a network must integrate information from multiple inputs, and how this information is encoded (e.g. redundantly between multiple sources, or uniquely by a single source) is crucial to the understanding of how neuronal networks transmit information. Information theory provides robust measures of the interdependence of multiple variables, and recent work has attempted to disentangle the different types of interactions captured by these measures (Fig 1A).

Fig. 1

a Let x,y be neurons which determine z. b The Information Decomposition (ID) breaks information into unique, redundant and synergistic components. c Delta theory maps functions onto a space which encodes the ID. d [3] calculates the ID via an optimization which we map to delta-space, and is solved by the points from [6]. This identifies the function by which z integrates information

Full size image

The Information Decomposition of Williams and Beer proposed decomposing the mutual information into unique, redundant, and synergistic components [1, 2]. This has been fruitfully applied, particularly in computational neuroscience, but there is no generally accepted method for its computation. Bertschinger et al. [3] developed one particularly rigorous approach, but it requires an intensive optimization over probability space (Fig 1B).

Independently, the quantitative genetics community has developed the Information Delta measures for detecting non-pairwise interactions for use in genetic datasets [4, 5, 6]. This has been exhaustively characterized for the discrete variables often found in genetics, yielding a geometric interpretation of how an arbitrary discrete function maps onto delta-space, and what its location therein encodes about the interaction (Fig 1C); however, this approach still lacks certain generalizations.

In this paper, we show that the Information Decomposition and Information Delta frameworks are largely equivalent. We identify theoretical advances in each that can be immediately applied towards answering questions open in the other. For example, we find that the results of Bertschinger et al. answer an open question in the Information Delta framework, specifically how to address the problem of linkage disequilibrium dependence in genetic data. We develop a method to computationally map the probability space defined by Bertschinger et al. into the space of delta measures, in which we can define a plane to which it is constrained with a well-defined optimum (Fig 1D). These optima occur at points in delta space which correspond to known discrete functions. This geometric mapping can thereby both side-step an expensive optimization and characterize the functional relationships between neurons. This unification of theoretical frameworks provides valuable insights for the analysis of how neurons integrate upstream information.

References

1. 1.
   Williams PL, Beer RD. Nonnegative decomposition of multivariate information. arXiv 2010, arXiv:1004.2515.
2. 2.
   Lizier JT, Bertschinger N, Jost J, Wibral M. Information decomposition of target effects from multi-source interactions: Perspectives on previous, current and future work. Entropy 2018, 20, 307.
3. 3.
   Bertschinger N, Rauh J, Olbrich E, Jost J, Ay N. Quantifying unique information. Entropy 2014, 16, 2161–2183.
4. 4.
   Galas D, Sakhanenko NA, Skupin A, Ignac T. Describing the complexity of systems: Multivariable “set complexity” and the information basis of systems biology. J Comput Biol. 2014, 2, 118–140.
5. 5.
   Sakhanenko NA, Galas DJ. Biological data analysis as an information theory problem: Multivariable dependence measures and the shadows algorithm. J Comput Biol. 2015, 22, 1005–1024.
6. 6.
   Sakhanenko NA, Kunert-Graf JM, Galas DJ. The information content of discrete functions and their application in genetic data analysis. J Comp Biol. 2017, 24, 1153–1178.

P89 Homeostatic mechanism of myelination for age-dependent variations of axonal conductance speed in the pathophysiology of Alzheimer’s disease

Maurizio De Pittà1, Giulio Bonifazi1, Tania Quintela-López2, Carolina Ortiz-Sanz2, María Botta2, Alberto Pérez-Samartín2, Carlos Matute2, Elena Alberdi2, Adhara Gaminde-Blasco2

1Basque Center for Applied Mathematics, Group of Mathematical, Computational and Experimental Neuroscience, Bilbao, Spain; 2Achucarro Basque Center for Neuroscience, Leioa, Spain

Correspondence: Giulio Bonifazi (gbonifazi@bcamath.org)

BMC Neuroscience 2019, 20(Suppl 1):P89

The structure of white matter in patients affected by Alzheimer’s disease (AD) and age-related dementia, typically reveals aberrant myelination, suggesting that ensuing changes in axonal conduction speed could contribute to cognitive impairment and behavioral deficits observed in those patients. Experiments ex vivo in a murine model of AD confirm these observations but also pinpoint to multiple, coexisting mechanisms that could intervene in regulation and maintenance of integrity of myelinated fibers. Density of myelinated fibers in the corpus callosum indeed appears not to be affected by disease progression in transgenic mice whereas density of myelinating oligodendrocyte is increased with respect to wild-type animals. Significantly, this enhancement correlates with an increased expression of myelin basic protein (MBP); as well as with nodes of Ranvier that are shorter and more numerous; and a decrease in axonal conduction speed. We show that these results can be reproduced by a classical model of action potential propagation in myelinated axons by the combination of three factors that are: (i) a reduction of node length in association with (ii) an increase of both internode number and (iii) myelin thickness. In the simple scenario of two interacting neural populations where a recently-observed inhibitory feedback on the degree of myelination is incorporated as a function of synaptic connection disrupted by extracellular amyloid beta oligomers (Aβ1-42), we show that the reduction of axonal conduction speed by the concerted increase of Ranvier’s node number and myelin thickness accounts for minimizing the energetic cost of interacting population activity.