28th Annual Computational Neuroscience Meeting: CNS*2019 | BMC Neuroscience | Full Text

28th Annual Computational Neuroscience Meeting: CNS*2019 | BMC Neuroscience | Full Text

P90 Collective dynamics of a heterogeneous network of active rotators

Pablo Ruiz, Jordi Garcia-Ojalvo

Universitat Pompeu Fabra, Department of Experimental and Health Sciences, Barcelona, Spain

Correspondence: Pablo Ruiz (pabloruizibarrechevea@gmail.com)

BMC Neuroscience 2019, 20(Suppl 1):P90

We analyze the behavior of a network of active rotators [1] containing both oscillatory and excitable elements. We assume that the oscillatory character of the elements is continuously distributed. The system exhibits three main dynamical behaviors (i) a quiescent phase in which all elements are stationary, (ii) global oscillations in which all elements oscillate in a synchronized manner, and (iii) partial oscillations in which a fraction of the units oscillates, partially synchronized among them (analogous to the case in [2]). We also observe that the pulse duration is shorter for the excitable units than for the oscillating ones, even though the former has smaller intrinsic frequencies than the latter. Apart from the standard usage of the Kuramoto order parameter (or its variance) as a measure of synchrony, and consequently, as a measure of the macroscopic state of the system, we are interested in finding an observable that helps gain insight on what is the position within a hierarchy of states. We can call this measure the potential or energy of the system, and define it as the integral over the phases, by gradient dynamics [3]. This variable can be considered as a measure of multistability. We also study more complex coupling situations, included the existence of negative links between coupled elements in a whole-brain network, mimicking the inhibitory connections present in the brain.

References

1. 1.
   Sakaguchi H, Shinomoto S, Kuramoto Y. Phase transitions and their bifurcation analysis in a large population of active rotators with mean-field coupling. Progress of Theoretical Physics 1988 Mar 1;79(3):600–7.
2. 2.
   Pazó D, Montbrió E. Universal behavior in populations composed of excitable and self-oscillatory elements. Physical Review E 2006 May 31;73(5):055202.
3. 3.
   Ionita F, Labavić D, Zaks MA, Meyer-Ortmanns H. Order-by-disorder in classical oscillator systems. The European Physical Journal B 2013 Dec 1;86(12):511.

P91 A hidden state analysis of prefrontal cortex activity underlying trial difficulty and erroneous responses in a distance discrimination task

Danilo Benozzo1, Giancarlo La Camera2, Aldo Genovesio1

1Sapienza University of Rome, Department of Physiology and Pharmacology, Rome, Italy; 2Stony Brook University, Department of Neurobiology and Behavior, Stony Brook, NY, United States of America

Correspondence: Danilo Benozzo (danilo.benozzo@uniroma1.it)

BMC Neuroscience 2019, 20(Suppl 1):P91

Previous studies have established the involvement of prefrontal cortex (PFC) neurons in the decision process during a distance discrimination task. However, no single-neuron correlates of important task variables such as trial difficulty was found. Here, we perform a trial-by-trial analysis of ensembles of simultaneously recorded neurons, specifically, multiple single-unit data from two rhesus monkeys performing the distance discrimination task. The task consists in the sequential presentation of two visual stimuli (S1 and S2, in this order) separated by a temporal delay. The monkeys had to report which stimulus was farthest from a reference point after a GO signal consisting in the presentation of the same two stimuli in the two sides of the screen. Six stimulus distances were tested (from 8 to 48mm), generating five levels of difficulty, each measured as the difference |S2-S1| between the relative positions of the stimuli (difficulty increases with |S2-S1|).

We analyzed the neural ensemble data with a Poisson hidden Markov model (HMM). A Poisson-HMM describes the activity of each single trial by a sequence of vectors of firing rates across simultaneously recorded neurons. Each vector of firing rates is a metastable ‘state’ of the neural activity. HMM allows to identify changes in neural state independently of external triggers, which have previously been linked to states of attention, expectation and decision making, to name a few.

For each experimental session, we fit the HMM to the neural ensemble starting from random initial conditions and different numbers of states (between 2 and 5) using maximum likelihood (Baum-Welch algorithm). The fitting procedure was repeated 5 times with new random initial conditions until a convergence criterion was reached (capped at 500 iterations). The model with the smallest BIC was selected as the best model. Post-fitting, a state was assigned to each 5ms bin of data if its posterior probability given the data exceeded 0.8. To further avoid overfitting, only states exceeding 0.8 for at least 50 consecutive ms were kept.

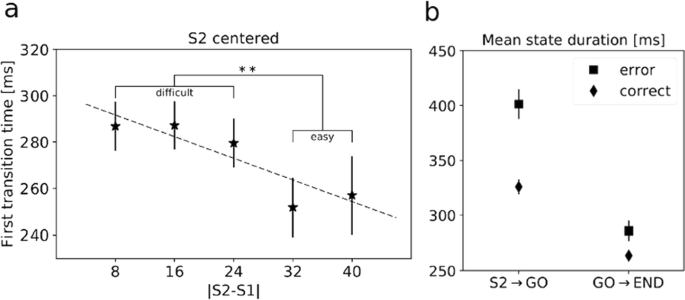
First, we looked for a relationship between trial difficulty and the first state transition time after S2 presentation. We found that faster state transitions occurred in easier trials (Fig. 1a), but no correlation was found with first transition times after the GO signal. This demonstrates that task difficulty modulates the neural dynamics during decisions, and this modulation occurs in the deliberation phase and is absent when the monkeys convert the decision into action.

Fig. 1

a First transition time after S2 evaluated across trial difficulties |S2-S1|. Higher |S2-S1| means lower difficulty. Dashed line is the linear regression interpolation (p<0.05). **=p<0.01, Welch’s t-test. b Mean state duration computed before and after the GO signal on correct and incorrect trials (2-way ANOVA, significant interaction and effects of trial type and time interval; p<0.001)

Full size image

Second, we found that RTs were significantly longer in error trials compared to correct trials overall (p<0.001, t-test). Thus, we investigated the relationship between reaction times and neural dynamics. We focused on a larger time window, from 400 ms before S2 until the beginning of the following trial, in order to better capture the whole dynamics of state transitions. We found longer mean state durations after S2 in error trials compared to correct trials (Fig. 1b), a signature of a slowing down of cortical dynamics during error trials. The effect was largest in the period from S2 to the GO signal, i.e., during the deliberation period (2-way ANOVA, interaction term, p<0.001). These results indicate a global slowdown of the neural dynamics prior to errors as the neural substrate of longer reaction times during incorrect trials.

P92 Neural model of the visual recognition of social interactions

Mohammad Hovaidi-Ardestani, Martin Giese

Hertie Institute for Clinical Brain Research, Centre for Integrative Neuroscience, Department of Cognitive Neurology, University Clinic Tübingen, Tübingen, Germany

Correspondence: Mohammad Hovaidi-Ardestani (mohammad.hovaidi-ardestani@uni-tuebingen.de)

BMC Neuroscience 2019, 20(Suppl 1):P92

Humans are highly skilled at interpreting intent or social behavior from strongly impoverished stimuli [1]. The neural circuits that derive such judgements from image sequences are entirely unknown. It has been hypothesized that this visual function is based on high-level cognitive processes, such as probabilistic reasoning. Taking an alternative approach, we show that such functions can be accomplished by relatively elementary neural networks that can be implemented by simple physiologically plausible neural mechanisms, forming a hierarchical (deep) neural model of the visual pathway.

Methods: Extending classical biologically-inspired models for object and action perception [2, 3] and alternatively a front-end that exploits a deep learning model (VGG16) for the construction of low and mid-level feature detectors, we built a hierarchical neural model that reproduces elementary psychophysical results on animacy and social perception from abstract stimuli. The lower hierarchy levels of the model consist of position-variant neural feature detectors that extract orientation and intermediately complex shape features. The next-higher level is formed by shape-selective neurons that are not completely position-invariant, which extract the 2D positions and orientation of moving agents. A second pathway analyses the 2D motion of the moving agents, exploiting motion energy detectors. Exploiting a gain-field network, we compute the relative positions of the moving agents and analyze their relative motion. The top layers of the model combine the mentioned features that characterize the speed and smoothness of motion, and spatial relationships of the moving agents. The highest level of the model consists of neurons that compute the perceived agency of the motions, and that classify different categories of social interactions.

Results: Based on input video sequences, the model successfully reproduces results of [4] on the dependence of perceived animacy on motion parameters, and its dependence on the alignment of motion and body axis. The model reproduces the fact that a moving figure that with a body axis, like a rectangle, result in stronger perceived animacy than a moving circle if the body axis is aligned with the motion direction. In addition, the model classifies different interactions from abstract stimuli, including six categories of social interactions that have been frequently tested in the psychophysical literature (following, fighting, chasing, playing, guarding, and flirting) (e.g. [5, 6]).

Conclusion: Using simple physiologically plausible neural circuits, the model accounts simultaneously for a variety of effects related to animacy and social interaction perception. Even in its simple form the model proves that animacy and social interaction judgements partly can be derived by very elementary operations within a hierarchical neural vision system, without a need of sophisticated probabilistic inference mechanisms. The model makes precise predictions about the tuning properties of different types of neurons that should be involved in the visual processing of such stimuli. Such predictions might serve as starting point for physiological experiments that investigate the correlate of the perceptual processing of animacy and interaction at the single-cell level.

References

1. 1.
   Heider F, Simmel M. An experimental study of apparent behavior. The American journal of psychology 1944 Apr 1;57(2):243–59. https://doi.org/10.2307/1416950
2. 2.
   Riesenhuber M, Poggio T. Hierarchical models of object recognition in cortex. Nature neuroscience 1999 Nov;2(11):1019. https://doi.org/10.1038/14819
3. 3.
   Giese MA, Poggio T. Cognitive neuroscience: neural mechanisms for the recognition of biological movements. Nature Reviews Neuroscience 2003 Mar;4(3):179. https://doi.org/10.1038/nrn1057
4. 4.
   Tremoulet PD, Feldman J. Perception of animacy from the motion of a single object. Perception 2000 Aug;29(8):943–51.
5. 5.
   Gao T, Scholl BJ, McCarthy G. Dissociating the detection of intentionality from animacy in the right posterior superior temporal sulcus. Journal of Neuroscience 2012 Oct 10;32(41):14276–80.
6. 6.
   McAleer P, Pollick FE. Understanding intention from minimal displays of human activity. Behavior Research Methods 2008 Aug 1;40(3):830–9. https://doi.org/10.3758/BRM.40.3.830

P93 Learning of generative neural network models for EMG data constrained by cortical activation dynamics

Alessandro Salatiello, Martin Giese

Center for Integrative Neuroscience & University Clinic Tübingen, Dept of Cognitive Neurology, Tübingen, Germany

Correspondence: Alessandro Salatiello (alessandro.salatiello@uni-tuebingen.de)

BMC Neuroscience 2019, 20(Suppl 1):P93

Recurrent Artificial Neural Networks (RNNs) are popular models for neural structures in motor control. A common approach to build such models is to train RNNs to reproduce the input-output mapping of biological networks. However, this approach suffers from the problem that the internal dynamics of such networks are typically highly under-constrained: even though they correctly reproduce the desired input-output behavior, their internal dynamics are not under control and usually deviate strongly from those of real neurons. Here, we show that it is possible to accomplish the dual goal of both reproducing the target input-output behavior and constraining the internal dynamics to be similar to the ones of real neurons. As a test-bed, we simulated an 8-target reaching task; we assumed that a network of 200 primary motor cortex (M1) neurons generates the necessary activity to perform such tasks in response to 8 different inputs and that this activity drives the contraction of 10 different arm muscles. We further assumed to have access to only a sample of M1 neurons (30%) and relevant muscles (40%). In particular, we first generated multiphasic EMG-like activity by drawing samples from a Gaussian process. Secondly, we generated ground truth M1-like activity by training a stability-optimized circuit (SOC) network [2] to reproduce the EMG activity through gain modulation [1]. Finally, we trained two RNN models with the full-FORCE method [3] to reproduce the subset of observed EMG activity; critically, while one of the networks (FF) was free to reach such a goal through the generation of arbitrary dynamics, the other (FFH) was constrained to do so by generating, through its recurrent dynamics, activity patterns resembling those of the observed SOC neurons. To assess the similarity between the activities of FF, FFH and SOC neurons, we applied canonical correlation analysis (CCA) on the latent factors extracted through PCA. This analysis revealed that while both the FF and FFH network were able to reproduce the EMG activities accurately, the FFH network, that is the one with constrained internal dynamics, showed a greater similarity in the neural response space with the SOC network. Such similarity is noteworthy since the sample used to constrain the internal dynamics was small. Our results suggest that this approach might facilitate the design of neural network models that bridge multiple hierarchical levels in motor control, at the same time including details of available single-cell data.

Acknowledgements: Funding from BMBF FKZ 01GQ1704, DFG GZ: KA 1258/15-1; CogIMon H2020 ICT-644727, HFSP RGP0036/2016, KONSENS BW Stiftung NEU007/1

References

1. 1.
   Stroud JP, Porter MA, Hennequin G, Vogels TP. Motor primitives in space and time via targeted gain modulation in cortical networks. Nature Neuroscience 2018 Dec;21(12):1774.
2. 2.
   Hennequin G, Vogels TP, Gerstner W. Optimal control of transient dynamics in balanced networks supports generation of complex movements. Neuron 2014 Jun 18;82(6):1394–406.
3. 3.
   DePasquale B, Cueva CJ, Rajan K, Abbott LF. full-FORCE: A target-based method for training recurrent networks. PloS One 2018 Feb 7;13(2):e0191527.

P94 A neuron can make reliable binary, threshold gate like, decisions if and only if its afferents are synchronized.

Timothee Masquelier1, Matthieu Gilson2

1CNRS, Toulouse, France; 2Universitat Pompeu Fabra, Center for Brain and Cognition, Barcelona, Spain

Correspondence: Timothee Masquelier (timothee.masquelier@cnrs.fr)

BMC Neuroscience 2019, 20(Suppl 1):P94

Binary decisions are presumably made by weighing and comparing evidence, which can be modeled using the threshold gate formalism: the decision depends on whether or not a weighted sum of input variables S exceeds a threshold θ. Incidentally, this is exactly how the first neuron model proposed by McCulloch and Pitts in 1943, and later used in the perceptron, worked. But can biological neurons implement such a function, assuming that the input variables are the afferent firing rates? This matter is unclear, because biological neurons deal with spikes, not firing rates.

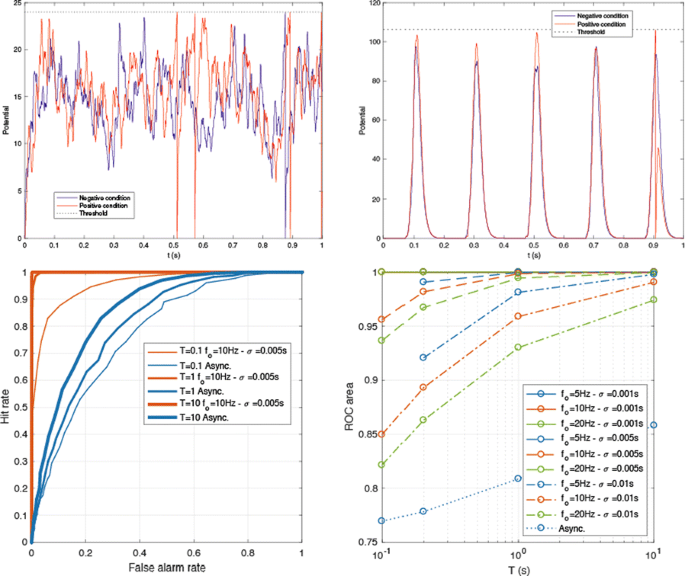
We investigated this issue through analytical calculations and numerical simulations, using a leaky integrate-and-fire (LIF) neuron (with τ  =  10 ms). The goal was to adjust the LIF’s threshold so that it fires at least one spike over a period T if S>θ (“positive condition”), and none otherwise (“negative condition”). We considered two different regimes: input spikes were either asynchronous (i.e., latencies were uniformly distributed over [0; T]), or synchronous. In the latter case, the spikes arrived in discrete periodic volleys (with frequency fo), and with a certain dispersion inside each volley (σ). As Fig. 1 Top shows, in the asynchronous regime any threshold will lead to false alarms and/or misses. Conversely, in the synchronous regime, it is possible to set a threshold that will be reached in the positive condition, but not in the negative one.

Fig. 1

(Top left) The asynchronous regime. Threshold = 24 causes a hit for the positive condition, but also a false alarm for the negative one. (Top right) The synchronous regime. Threshold = 105 causes a hit for the positive condition, and no false alarm for the negative one. (Bottom left) Examples of ROC curves. (Bottom right) ROC area as a function of T, in the asynchronous and synchronous conditions

Full size image

To demonstrate this more rigorously, we computed the receiver operating characteristic (ROC) curve as a function of T in both regimes (Fig. 1 Bottom). For the synchronous regime, we varied fo and σ. In short, the asynchronous regime leads to poor accuracy, which increases with T, but very slowly. Conversely, the synchronous regime leads to much better accuracy, which increases with T, but decreases with σ and fo.

In conclusion, if the decision needs to be taken in a reasonable amount of time, only the synchronous regime is viable, and the precision of the synchronization should be in the millisecond range. We are now exploring more biologically realistic regimes in which only a subset of the afferents is synchronized, in between the two extreme examples in Fig. 1. In the brain, the required synchronization could come from abrupt changes in the environment (e.g., stimulus onset), active sampling (e.g., saccades and microsaccades, sniffs, licking, touching), or endogenous brain oscillations. For example, rhythms in the beta or gamma ranges that correspond to different values for fo lead to different efficiency in our scheme for transmitting information, which implies constraints on the volley precision σ.

P95 Unifying network descriptions of neural mass and spiking neuron models and specifying them in common, standardized formats

Jessica Dafflon1, Angus Silver2, Padraig Gleeson2

1King’s College London, Centre for Neuroimaging Sciences, London, United Kingdom; 2University College London, Dept. of Neuroscience, Physiology & Pharmacology, London, United Kingdom

Correspondence: Padraig Gleeson (p.gleeson@ucl.ac.uk)

BMC Neuroscience 2019, 20(Suppl 1):P95

Due to the inherent complexity of information processing in the brain, many different approaches have been taken to creating models of neural circuits, each making different choices about the level of biological detail to incorporate and the mathematical/analytical tractability of the models. Some approaches favour investigating large scale, brain wide behaviour with interconnected populations, each representing the activity of many neurons. Others include many of the known biophysical details of the constituent cells, down to the level of ion channel kinetics. These different approaches often lead to disjointed communities investigating the same system from very different perspectives. There is also an important issue of different simulation technologies being used in each of these communities (e.g. The Virtual Brain; NEURON), further preventing exchange of models and theories.

To address these issues, we have extended the NeuroML model specification language [1, 2], which already supports descriptions of networks of biophysically complex, conductance based cells, to allow descriptions of population units where the average activity of the cells is given by a single variable. With this, it is possible to describe classic models such as that of Wilson and Cowan [3] in the same format as more detailed models. To demonstrate the utility of this approach we have converted a recent large-scale network model of the macaque cortex [4] into NeuroML format. This model features the interaction between the feedforward and feedback signalling across multiple scales. In particular, interactions inside cortical layers, between layers, between areas and at the whole cortex level are simulated. With the NeuroML implementation we were able to replicate the main findings described in the original paper.

Compatibility with NeuroML comes with other advantages, particularly the ability to visualise the structure of models in the format in 3D on Open Source Brain [5] as well as analyse the network connectivity and run and replay simulations (http://www.opensourcebrain.org/projects/mejiasetal2016). This extension to NeuroML for neural mass models, the support in compatible tools and platforms and example networks in this format will help enable sharing, comparison and reuse of models between researchers taking diverse approaches to understanding the brain.

References

1. 1.
   Cannon RC, Gleeson P, Crook S, Ganapathy G, Marin B, Piasini E, et al. LEMS: A language for expressing complex biological models in concise and hierarchical form and its use in underpinning NeuroML 2. Frontiers in neuroinformatics 2014;8. https://doi.org/10.3389/fninf.2014.00079
2. 2.
   Gleeson P, Crook S, Cannon RC, Hines ML, Billings GO, Farinella M, et al. NeuroML: A Language for Describing Data Driven Models of Neurons and Networks with a High Degree of Biological Detail. PLoS Comput Biol. Public Library of Science 2010;6: e1000815.
3. 3.
   Wilson HR, Cowan JD. Excitatory and inhibitory interactions in localized populations of model neurons. Biophys J. 1972;12: 1–24.
4. 4.
   Mejias JF, Murray JD, Kennedy H, Wang X-J. Feedforward and feedback frequency-dependent interactions in a large-scale laminar network of the primate cortex. Science advances 2016;2: e1601335.
5. 5.
   Gleeson P, Cantarelli M, Marin B, Quintana A, Earnshaw M, Piasini E, et al. Open Source Brain: a collaborative resource for visualizing, analyzing, simulating and developing standardized models of neurons and circuits. bioRxiv 2018; 229484.

P96 NeuroFedora: a ready to use Free/Open Source platform for Neuroscientists

Ankur Sinha1, Luiz Bazan2, Luis M. Segundo2, Zbigniew Jędrzejewski-Szmek2, Christian J. Kellner2, Sergio Pascual2, Antonio Trande2, Manas Mangaonkar2, Tereza Hlaváčková2, Morgan Hough2, Ilya Gradina2, Igor Gnatenko2

1University of Hertfordshire, Biocomputation Research Group, Hatfield, United Kingdom; 2Fedora Project

Correspondence: Ankur Sinha (a.sinha2@herts.ac.uk)

BMC Neuroscience 2019, 20(Suppl 1):P96

Modern Neuroscience relies heavily on software. From the gathering of data, simulation of computational models, analysis of large amounts of information, to collaboration and communication tools for community development, software is now a necessary part of the research pipeline.

While the Neuroscience community is gradually moving to the use of Free/Open Source Software (FOSS) [11], our tools are generally complex and not trivial to deploy. In a community that is as multidisciplinary as Neuroscience, a large chunk of researchers hails from fields other than computing. It, therefore, often demands considerable time and effort to install, configure, and maintain research tool sets.

In NeuroFedora, we present a ready to use, FOSS platform for Neuroscientists. We leverage the infrastructure resources of the FOSS Fedora community [3] to develop a ready to install operating system that includes a plethora of Neuroscience software. All software included in NeuroFedora is built in accordance with modern software development best practices, follows the Fedora community’s Quality Assurance process, and is well integrated with other software such as desktop environments, text editors, and other daily use and development tools.

While work continues to make more software available in NeuroFedora covering all aspects of Neuroscience, NeuroFedora already provides commonly used Computational Neuroscience tools such as the NEST simulator [12], GENESIS [2], Auryn [8], Neuron [1], Brian (v1 and 2) [5], Moose [4], Neurord [10], Bionetgen [9], COPASI [6], PyLEMS [7], and others.

With up to date documentation atneuro.fedoraproject.org, we invite researchers to use NeuroFedora in their research and to join the team to help NeuroFedora better aid the research community.

References

1. 1.
   Hines ML, Carnevale NT. The NEURON simulation environment. Neural computation 1997 Aug 15;9(6):1179–209.
2. 2.
   Bower JM, Beeman D, Hucka M. The GENESIS simulation system, 2003.
3. 3.
   RedHat. Fedora Project, 2008.
4. 4.
   Dudani N, Ray S, George S, Bhalla US. Multiscale modeling and interoperability in MOOSE. BMC Neuroscience 2009 Sep;10(1):P54.
5. 5.
   Goodman DF, Brette R. The Brian simulator. Frontiers in neuroscience 2009 Sep 15; 3:26.
6. 6.
   Mendes P, Hoops S, Sahle S, et al. Computational modeling of biochemical networks using COPASI. Methods in molecular biology (Clifton, N.J.) 2009 500, 17–59. ISSN: 1064–3745.
7. 7.
   Vella M, Cannon RC, Crook S, et al. libNeuroML and PyLEMS: using Python to combine procedural and declarative modeling approaches in computational neuroscience. Frontiers in neuroinformatics 2014 Apr 23;8:38.
8. 8.
   Zenke F, Gerstner W. Limits to high-speed simulations of spiking neural networks using general-purpose computers. Frontiers in neuroinformatics 2014 Sep 11;8:76.
9. 9.
   Harris LA, Hogg JS, Tapia JJ, Sekar JA, Gupta S, Korsunsky I, Arora A, Barua D, Sheehan RP, Faeder JR. BioNetGen 2.2: advances in rule-based modeling. Bioinformatics 2016 Jul 8;32(21):3366–8.
10. 10.
    Jȩdrzejewski-Szmek Z, Blackwell KT. Asynchronous τ-leaping. The Journal of chemical physics 2016 Mar 28;144(12):125104.
11. 11.
    Gleeson P, Davison AP, Silver RA, Ascoli GA. A commitment to open source in neuroscience. Neuron 2017 Dec 6;96(5):964–5.
12. 12.
    Linssen C, Lepperød ME, Mitchell J, et al. NEST 2.16.0 Aug. 2018-08. https://doi.org/10.5281/zenodo.1400175.

P97 Flexibility of patterns of avalanches in source-reconstructed magnetoencephalography

Pierpaolo Sorrentino1, Rosaria Rucco2, Fabio Baselice3, Carmine Granata4, Rosita Di Micco5, Alesssandro Tessitore5, Giuseppe Sorrentino2, Leonardo L Gollo1

1QIMR Berghofer Medical Research Institute, Systems Neuroscience Group, Brisbane, Australia; 2University of Naples Parthenope, Department of movement science, Naples, Italy; 3University of Naples Parthenope, Department of Engineering, Naples, Italy; 4National Research Council of Italy, Institute of Applied Sciences and Intelligent Systems, Pozzuoli, Italy; 5University of Campania Luigi Vanvitelli, Department of Neurology, Naples, Italy

Correspondence: Pierpaolo Sorrentino (ppsorrentino@gmail.com)

BMC Neuroscience 2019, 20(Suppl 1):P97

Background: In many complex systems, when an event occurs, other units follow, giving rise to a cascade. The spreading of activity can be quantified by the branching ratio σ, defined by the number of active units at the present time over the one at the previous time step [1]. If σ = 1, the system is critical. In neuroscience, a critical system is believed to be more efficient [2]. For a critical branching, the system will visit a higher number of states [3]. Utilizing MEG recordings, we characterize patterns of activity at the whole brain level, and we compare the flexibility of patterns observed in healthy controls and Parkinson’s disease (PD). We hypothesize that the damages to the neuronal circuitry will move the network to a less efficient and flexible state, and that this may indicate clinical disability.

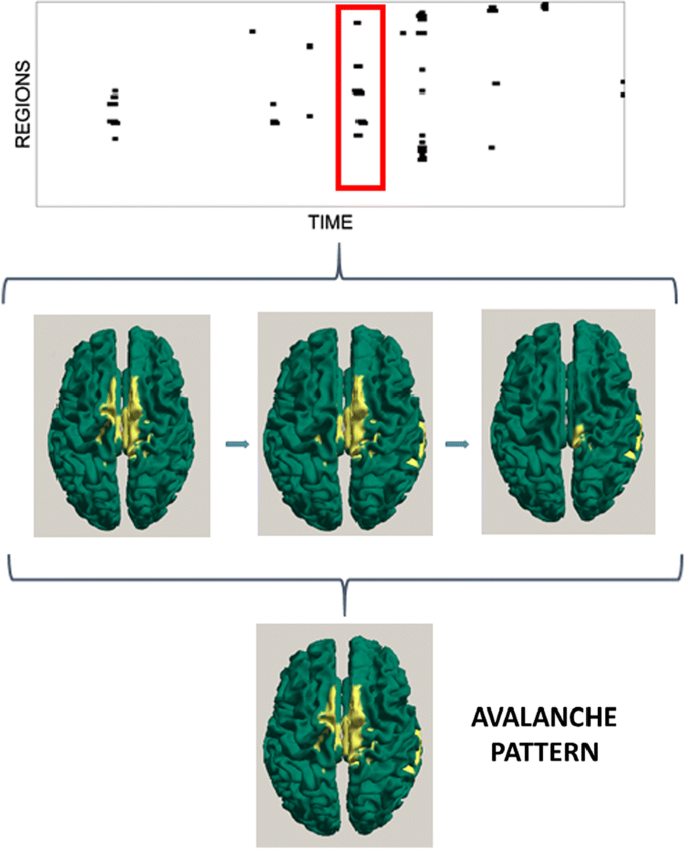
Methods: We recorded five minutes of closed eyes resting-state MEG in two cohorts: thirty-nine PD patients (20 males and 19 females, age 64.87 ± 9.12 years) matched with thirty-eight controls (19 males and 19 females, age 62.35 ± 8.74 years). The source-level time series of neuronal activity were reconstructed in 116 regions, by a beamformer approach based on the native MRI. The time series were filtered in the classical frequency bands. An avalanche was defined as a continuous sequence of time bins with activity on any region. T σ was estimated based on the geometric mean. We then counted the number of different patterns of avalanches that were present in each subject, and compared them between groups by permutation testing (Fig. 1). Finally, the clinical state was evaluated using the UPDRS-III scale. The relationship occurring between the number of patterns a patient visited and its clinical phenotype was assessed using linear correlation.

Fig. 1

a Reconstructed MEG time series. b Z-scores of each time series, binarized as abs(z) > 3. c Binarized time series, red rectangle is an avalanche. d Active regions (yellow) in an avalanche. e Avalanche pattern: any area active in any moment during the avalanche. f All individual patterns that have occurred (i.e. no pattern repetition is shown in this plot)

Full size image

Results: Firstly, the analysis of sigma shows that MEG signals are in the critical state. Furthermore, the frequency band analysis showed that criticality is not a frequency-specific phenomenon. However, the contribution of each region to the avalanche patterns was frequency specific A comparison between healthy controls and PD patients shows that the latter tend to visit a lower number of patterns (for broad band p = 0.0086). The lower the number of visited patterns, the greater their clinical impairment.

Discussion: Here we put forward a novel way to identify brain states and quantify their flexibility. The contribution of regions to the diversity of patterns is heterogeneous and frequency specific, giving rise to frequency specific topologies Although the number of patterns of activity observed across participants is varied, we found that they are substantially reduced in the PD patients. Moreover, the amount of such reduction is significantly associated with the clinical disability.

References

1. 1.
   Kinouchi O, Copelli M. Optimal dynamical range of excitable networks at criticality. Nature physics 2006 May;2(5):348.
2. 2.
   Cocchi L, Gollo LL, Zalesky A, Breakspear M. Criticality in the brain: A synthesis of neurobiology, models and cognition. Progress in neurobiology 2017 Nov 1;158:132-52.
3. 3.
   Haldeman C, Beggs JM. Critical branching captures activity in living neural networks and maximizes the number of metastable states. Physical review letters 2005 Feb 7;94(5):058101.

P98 A learning mechanism in cortical microcircuits for estimating the statistics of the world

Jordi-Ysard Puigbò Llobet1, Xerxes Arsiwalla1, Paul Verschure2, Miguel Ángel González-Ballester3

1Institute for Bioengineering of Catalonia, Barcelona, Spain; 2Institute for BioEngineering of Catalonia (IBEC), Catalan Institute of Advanced Studies (ICREA), SPECS Lab, Barcelona, Spain; 3UPF, ICREA, DTIC, Barcelona, Spain

Correspondence: Jordi-Ysard Puigbò Llobet (jysard@ibecbarcelona.eu)

BMC Neuroscience 2019, 20(Suppl 1):P98

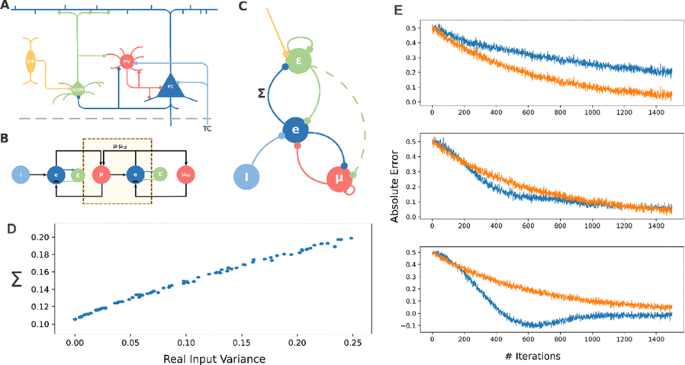
We know that the brain can estimate what is the expected value of an input signal. Up to some extent, signals that differ slightly from this expectation will be ignored, whereas errors that exceed some particular threshold will unavoidably convey a behavioral or physiological response. In this work, we assume that this threshold should be variable and therefore dependent on the input uncertainty. Consequently, we present here a biologically plausible model of how the brain can estimate uncertainty in sensory signals. In the predictive coding framework, our model will attempt to assess the validity of sensory predictions and regulate learning accordingly. In this work, we use gradient ascent to derive the formulation that defines a dynamical system which provides estimations of input data while also estimating their variance. We start with the assumption that the probability of our sensory input being explained by internal parameters of the model and other external signals follows a normal distribution. Similar to the approach of [1], we minimize the error in predicting the input signal but, instead of fixing the standard deviation to one static value, we estimate the variance of the input online, as a parameter in our dynamical system. The resulting model is presented as a simple recurrent neural network in Fig. 1C (nodes change with the weighted sum of inputs and vertices follow Hebbian-like learning rules). This microcircuit becomes a model of how cortical networks use expectation maximization to estimate mean and variance of the input signals simultaneously (Fig. 1D). We carefully analyze the implications of estimating uncertainty in parallel to minimizing prediction error to observe that the computation of the variance results in the minimization of the relative error (absolute error divided by variance). While classical models of predictive coding assume the variance to be a fixed constant extracted from the data once, we observe that estimating the variance online increases considerably learning speed at the cost of sometimes converging to less accurate estimations (Fig. 1E). The learning process becomes more resilient to input noise than previous approaches while requiring accurate estimates of the expected input variance. We discuss that this system can be implemented under biological constraints. In that case, our model predicts that two different classes of inhibitory interneurons in the Neocortex must play a role in either estimating mean or variance and that external modulation of the variance-computing interneurons results in the modulation of learning speed, promoting the exploitation of existing models versus the adaptation of existing ones.

Fig. 1

a Cortical representation of our microcircuit model, drawn schematically in c. b extension beyond the Rao-Ballard model of predictive coding by our model. d A fairly linear profile in model estimated variance and real variance. e Shows the prediction error over time comparing our model (blue) and a standard gradient descent method (orange) for 3 initial estimates of variance

Full size image

P99 Generalization of frequency mixing and temporal interference phenomena through Volterra analysis

Nicolas Perez Nieves, Dan Goodman

Imperial College London, Electrical and Electronic Engineering, London, United Kingdom

Correspondence: Nicolas Perez Nieves (np1714@ic.ac.uk)

BMC Neuroscience 2019, 20(Suppl 1):P99

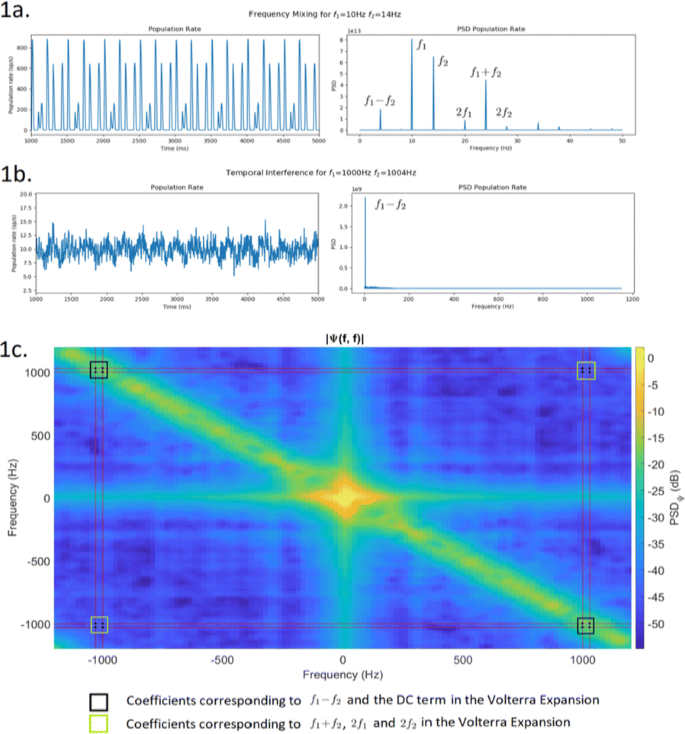
It has been recently shown that it is possible to use sinusoidal electric fields at kHz frequencies to enable focused, yet non-invasive, neural stimulation at depth by delivering multiple electric fields to the brain at slightly different frequencies (f1and f2) that are themselves too high to recruit effective neural firing, but for which the offset frequency is low enough to drive neural activity. This is called temporal interference (TI) [1]. However, it is not yet known the mechanism by which these electric fields are able to depolarise the cell membrane at the difference frequency despite the lack of depolarization by the individual kHz fields. There is some theoretical analysis into showing how neural stimulation at f1, f2<150Hz generates activity at the difference (f1-f2) and sum (f1+f2) of the frequencies due to the non-linearity of the spiking mechanism in neurons [2] via frequency mixing (FM). Yet, this approach is not general enough to explain why at higher frequencies we still see activity at the difference (f1-f2) with no activity present at any other frequency. To model the non-linearity present in neurons we propose using a Volterra expansion. First, we show that any non-linear system of order P when stimulated by N sinusoids will output a linear combination of sinusoids at frequencies given by all the possible linear combinations of the original frequencies with coefficients ±{0, 1, …, P}. This is consistent with [2] who give output frequencies at fout = nf1+mf2for n, m = ±{0, 1, 2}. We also show that the amplitude of each of the sinusoidal components at the output depends on the P-dimensional Fourier transforms of the Pth order kernel of the Volterra expansion evaluated at the stimulation frequencies (e.g. for a P = 2 system Ψ(±f{1, 2}, ±f{1, 2})) We simulate a population of leaky integrate and fire neurons stimulated by two sinusoidal currents at f1and f2and record the average population firing rate. For low frequencies (Fig. 1a), we see all combinations nf1+mf2as in [2]. For high frequencies (Fig. 1b), we only find f1-f2as in [1].

Fig. 1

a, b FM and TI respectively on 1000 LIF neurons. c PSD of the 2D-Fourier Transform of the second order Volterra kernel of a non-linear system consisting of the LIF neurons used in a and b explaining both FM and TI

Full size image

We then obtain the second order Volterra kernel using the Lee-Schetzen method [3]. The 2D Fourier transform of the kernel is shown in Fig. 1c. The dots show the 16 coefficients corresponding to |Ψ(±f{1, 2}, ±f{1, 2})|. As shown, for high stimulation frequencies, only the coefficients corresponding to f1-f2and the DC term are high enough to generate a response in the network, thus explaining TI stimulation. For low stimulation frequencies (<150Hz), all coefficients are high enough to produce a significant response at all nf1+mf2.

We have generalised previous experimental and theoretical results on temporal interference and frequency mixing. Understanding the mechanism of temporal interference stimulation will facilitate its clinical adoption, help develop improvement strategies and may reveal new computational principles of the brain.

References

1. 1.
   Grossman N, et al. Non-invasive Deep Brain Stimulation via Temporally Interfering Electric Fields. Cell 2017, Vol.169, Issue 6, pp.1029–1041.e16
2. 2.
   Haufler D, Pare D. Detection of Multiway Gamma Coordination Reveals How Frequency Mixing Shapes Neural Dynamics. Neuron 2019 Vol. 101, Issue 4, pp.603-614.e6
3. 3.
   van Drongelen, W. Signal Processing for Neuroscientists. Elsevier 2010, pp.39-90.

P100 Neural topic modelling

Pamela Hathway, Dan Goodman

Imperial College London, Department of Electrical and Electronic Engineering, London, United Kingdom

Correspondence: Pamela Hathway (p.hathway16@imperial.ac.uk)

BMC Neuroscience 2019, 20(Suppl 1):P100

Recent advances in neuronal recording techniques have led to the availability of large datasets of neuronal activity. This creates new challenges for neural data analysis methods: 1) scalability to larger numbers of neurons, 2) combining data on different temporal and spatial scales e.g. single units and local field potentials and 3) interpretability of the results.

We propose a new approach to these challenges: Neural Topic Modelling, a neural data analysis tool based on Latent Dirichlet Allocation (LDA), a method routinely used in text mining to find latent topics in texts. For Neural Topic Modelling, neural data is converted into the presence or absence of discrete events (e.g. neuron 1 has a higher firing rate than usual), which we call “neural words”. A recording is split into time windows that reflect stimulus presentation (“neural documents”) and the neural words present in each neural document are used as input to LDA. The result is a number of topics—probability distributions over words—which best explain the given occurrences of neural words in the neural documents.

To demonstrate the validity of Neural Topic Modelling we analysed an electrophysiological dataset of visual cortex neurons recorded with a Neuropixel electrode. The spikes were translated into four simple neural word types: 1) increased firing rate in neuron i, 2) decreased firing rate in neuron i, 3) small inter-spike intervals in neuron i, 4) neurons i and j are simultaneously active.

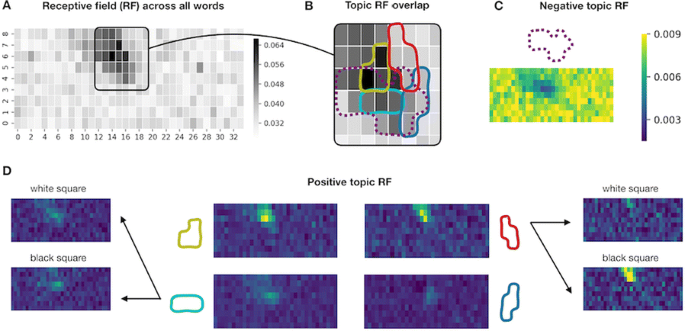
Neural Topic Modelling identifies topics in which the neural words are similar in their preferences for stimulus location and brightness. Five out of ten topics exhibited a clear receptive field (RF)—a small region to which the words in the topic responded preferentially (positive RF, see Fig. 1 D) or non-preferentially (negative RF, see Fig. 1 C) as measured by weighted mean probabilities of the appearance of topic words given the stimulus location. The topic receptive fields overlap with the general mean probability of a word occurring given the stimulus location (see Fig. 1 A), but the topics responded to different subregions (see Fig. 1 B) and some were brightness-sensitive (see Fig. 1 D, right). Additionally, topics seem to reflect proximity on the recording electrode. We confirmed that topic groupings were not driven by word order or overall word count.

Fig. 1

Topic receptive fields. a Probability of a word happening given stimulus location on the 9x34 grid. c, d Weighted mean probabilities for five topics with negative (c) and positive (d) receptive fields (RF). Colormap applies to C and D. Brightness sensitivity is shown for two topics (d left & right). b Overlap of pos. and neg. (dashed) RFs from topics in C & D masked at 0.8 of max value

Full size image

Neural Topic Modelling is an unsupervised analysis tool that receives no knowledge about the cortex topography nor about the spatial structure of the stimuli, but is nonetheless able to recover these relationships. The neural activity patterns used as neural words are interpretable by the brain and the resulting topics are interpretable by researchers. Converting neural activity into relevant events makes the method scalable to very large datasets and enables the analysis of neural data recordings on different spatial or temporal scales. It will be interesting to apply the model to more complex datasets e.g. in behaving mice, or to datasets where the neural representation of the stimulus structure is less clear e.g. for auditory or olfactory experiments.

The combination of scalability, applicability across temporal and spatial scales and the biological interpretability of Neural Topic Modelling sets this approach apart from other machine learning approaches to neural data analysis. We will make Neural Topic Modelling available to all researchers in the form of a Python software package.

P101 An attentional inhibitory feedback network for multi-label classification

Yang Chu, Dan Goodman

Imperial College London, Electrical Engineering, London, United Kingdom

Correspondence: Yang Chu (y.chu16@imperial.ac.uk)

BMC Neuroscience 2019, 20(Suppl 1):P101

It’s not difficult for people to distinguish the sound of a piano and a bass in a jazz ensemble, or to recognize an actor under unique stage lighting, even if these combinations have never been experienced before. However, these multi-label recognition tasks remain challenging for current machine learning and computational neural models. The first challenge is to learn to generalize along with the combinatorial explosion of novel combinations, in contrast to brute-force memorization. The second challenge is to infer the multiple latent causes from mixed signals.

Here we present a new attentional inhibitory feedback model as a first step to address both these challenges and study the impact of feedback connections on learning. The new model outperforms baseline feedforward-only networks in an overlapping-handwritten-digits recognition task. Our simulation results also provide new understanding of feedback guided synaptic plasticity and complementary learning systems theory.

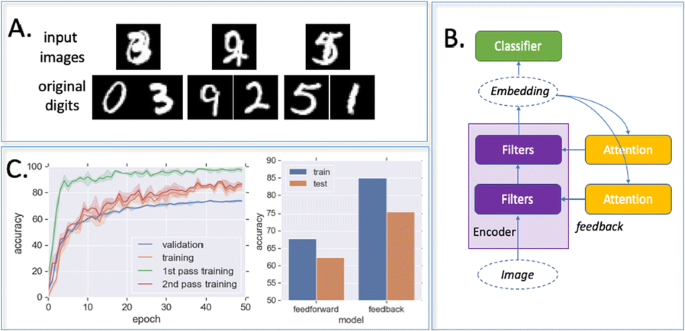
The task is to recognize two overlapping digits in an image (Fig 1A). The advantage of this for comparing neuro-inspired and machine learning approaches is that it is easy for humans but challenging for machine learning models, as they need to learn individual digits from combinations. Recognizing single handwritten digits, by contrast, can easily be solved by modern deep learning models.

Fig. 1

a Samples of input images for overlapping handwritten digit recognition task. b Attentional feedback network structure. c Left: Attentional feedback model learning process. Right: Performance comparison to feedforward-only baseline network

Full size image

The proposed model (Fig 1B) has a feature encoder built on a multi-layer fully connected neural network. Each encoder neuron receives an inhibitory feedback connection from a corresponding attentional neural network. During recognition, an image is first fed through the encoder, yielding a first guess. Then, based on the most confidently recognized digit, the attention module feeds back a multiplicative inhibitory signal to each encoder neuron. In the following time step, the image is processed again, but by the modulated encoder, resulting in a second recognition result. This feedback loop can carry on several times.

In our model, attention modulates the effective plasticity of different synapses based on the predicted contributions. While the attention networks learn to select more distinctive features, the encoder learns better with synapse-specific guidance from attention. Our feedback model achieves significantly higher accuracy comparing with the feedforward baseline network on both training and validation datasets (Fig 1C), despite having fewer neurons (2.6M compared to 3.7M). State of the art machine learning models can outperform our model but requires five to ten times as many parameters and more than a thousand times training data. Finally, we found intriguing dynamics during the co-learning process among attention and encoder networks, suggesting further links to neural development phenomena and memory consolidation in the brain.

Acknowledgements: This work was partly supported by a Titan Xp donated by the NVIDIA Corporation, and The Royal Society (grant RG170298).

P102 Closed-loop sinusoidal stimulation of ventral hippocampal terminals in prefrontal cortex preferentially entrains circuit activity at distinct frequencies

Maxym Myroshnychenko1, David Kupferschmidt2, Joshua Gordon3

1National Institutes of Health, National Institute of Neurological Disorders and Stroke, Bethesda, MD, United States of America; 2National Institute of Neurological Disorders and Stroke, Integrative Neuroscience Section, Bethesda, MD, United States of America; 3National Institutes of Health, National Institute of Mental Health, Bethesda, United States of America

Correspondence: Maxym Myroshnychenko (mmyros@gmail.com)

BMC Neuroscience 2019, 20(Suppl 1):P102

Closed-loop interrogation of neural circuits allows for causal description of circuit properties. Recent developments in recording and stimulation technology brought about the ability to stimulate or inhibit activity in one brain region conditional on the activity of another. Furthermore, the advent of optogenetics made it possible to control the activity of discrete, anatomically defined neural pathways. Normally, optogenetic excitation is induced using narrow pulses of light of the same intensity. To better approximate endogenous neural oscillations, we used continuously varied sinusoidal open- and closed-loop optogenetic stimulation of ventral hippocampal terminals in prefrontal cortex in awake mice. This allowed us to investigate the dynamical relationship between the two brain regions, which is critical for higher cognitive functions such as spatial working memory. Open-loop stimulation at different frequencies and amplitudes allowed us to map the response of the circuit over a range of parameters, revealing that response power in prefrontal and hippocampal field potentials was maximal in two tongue-shaped regions centered respectively at 8 Hz and 25–35 Hz, resembling resonant properties of coupled oscillators. Coherence between them was also maximal at these two frequency ranges. This suggests that neural activity in the circuit became entrained to the laser-induced oscillation, and the entrainment was not limited to the region near the stimulating laser. Further, adding frequency-filtered feedback based on the hippocampal field potential enhanced or suppressed synchronization depending on the amount of delay introduced to the feedback procedure. Specifically, delaying the optical stimulation relative to the hippocampal signal by about half of its period enhanced the entrainment of the prefrontal and hippocampal field potential responses to the stimulation frequency and enhanced prefrontal spikes’ phase locking to hippocampal field potential. On the other hand, closed-loop feedback without delay resulted in little enhancement and even decreased firing rate of prefrontal neurons. This is to our knowledge the first demonstration of an oscillatory phase-dependent bias in hippocampal-prefrontal communication based on an active closed-loop intervention. These results stand to inform computational models of communication between brain regions, and guide the use of continuously varying, closed-loop stimulation to assess effects of enhancing endogenous long-range neuronal communication on behavioral measures of cognitive function.

P103 The shape of thought: data-driven synthesis of neuronal morphology and the search for fundamental parameters of form

Joe Graham

SUNY Downstate Medical Center, Department of Physiology and Pharmacology, Brooklyn, NY, United States of America

Correspondence: Joe Graham (joe.w.graham@gmail.com)

BMC Neuroscience 2019, 20(Suppl 1):P103

Neuronal morphology is critical in the form and function of nervous systems. Morphological diversity in and between populations of neurons contributes to functional connectivity and robust behavior. Morphologically-realistic computational models are an important tool in improving our understanding of nervous systems. Continual improvements in computing make large-scale, morphologically-realistic, biophysical models of nervous systems increasingly feasible. However, reconstructing large numbers of neurons experimentally is not scalable. Algorithmic generation of neuronal morphologies (“synthesis” of “virtual” neurons) holds promise for deciphering underlying patterns in branching morphology as well as meeting the increasing need in computational neuroscience for large numbers of diverse, realistic neurons.

There are many ways to quantify neuronal form, not all are useful. [1] proposed that “from the mass of quantitative information available” a small set of “fundamental parameters of form” and their intercorrelations could be measured from reconstructed neurons which could potentially “completely describe” the population. A parameter set completely describing the original data would be useful for classification of neuronal types, exploring embryological development of neurons, and for understanding morphological changes following illness or intervention. [2] realized that virtual dendritic trees could be generated by stochastic sampling from a set of fundamental parameters (a synthesis model). Persistent differences between the reconstructed and virtual trees guided model refinement. [3] realized entire virtual neurons could be created by synthesizing multiple dendritic trees from a virtual soma. [3] implemented the models of Hillman and Burke et al. and made the code and data publicly available. Both groups used the same data set: a population of six fully-reconstructed cat alpha motoneurons. They were able to generate virtual motoneurons that were similar to the reconstructed ones, however, persistent, significant differences remained unexplained.

Exploration of these motoneurons and novel synthesis models led to two major insights into dendritic form. 1) Parameter distributions correlate with local properties, and these correlations must be accounted for in synthesis models. Dendritic diameter is an important local property, correlating with most parameters. 2) Parent branch parameters correlate differently than those of terminal branches, requiring setting a branch’s type before synthesizing it. Inclusion of these findings in a synthesis model produces virtual motoneurons that are far more similar to the reconstructions than previous models and which are statistically indistinguishable across most measures. These findings hold true across a variety of neuronal types, and may constitute a key to the elusive “fundamental parameters of form” for neuronal morphology.

References

1. 1.
   Hillman DE. Neuronal shape parameters and substructures as a basis of neuronal form. In: The Neurosciences, 4th Study program. Cambridge: MIT Press; 1979, pp. 477–498.
2. 2.
   Burke RE, Marks WB, Ulfhake B. A parsimonious description of motoneuron dendritic morphology using computer simulation. Journal of Neuroscience 1992, 12(6), pp. 2403–2416.
3. 3.
   Ascoli GA, Krichmar JL, Scorcioni R, Nasuto SJ, Senft SL, Krichmar GL. Computer generation and quantitative morphometric analysis of virtual neurons. Anatomy and Embryology 2001 Oct 1;204(4):283–301.

P104 An information-theoretic framework for examining information flow in the brain

Praveen Venkatesh, Pulkit Grover

Carnegie Mellon University, Electrical and Computer Engineering, Pittsburgh, PA, United States of America

Correspondence: Praveen Venkatesh (vpraveen@cmu.edu)

BMC Neuroscience 2019, 20(Suppl 1):P104

We propose a formal, systematic methodology for examining information flow in the brain. Our method is based on constructing a graphical model of the underlying computational circuit, comprising nodes that represent neurons or groups of neurons, which are interconnected to reflect anatomy. Using this model, we provide an information-theoretic definition for information flow, based on conditional mutual information between the stimulus and the transmissions of neurons. Our definition of information flow organically emphasizes what the information is about: typically, this information is encapsulated in the stimulus or response of a specific neuroscientific task. We also give pronounced importance to distinguishing the defining of information flow from the act of estimating it.

The information-theoretic framework we develop provides theoretical guarantees that were hitherto unattainable using statistical tools such as Granger Causality, Directed Information and Transfer Entropy, partly because they lacked a theoretical foundation grounded in neuroscience. Specifically, we are able to guarantee that if the “output” of the computational system shows stimulus-dependence, then there exists an “information path” leading from the input to the output, along which stimulus-dependent information flows. This path may be identified by performing statistical independence tests (or sometimes, conditional independence tests) at every edge. We are also able to obtain a fine-grained understanding of information geared towards understanding computation, by identifying which transmissions contain unique information and which are derived or redundant.

Furthermore, our framework offers consistency-checks, such as statistical tests for detecting hidden nodes. It also allows the experimentalist to examine how information about independent components of the stimulus (e.g., color and shape of a visual stimulus in a visual processing task) flow individually. Finally, we believe that our structured approach suggests a workflow for informed experimental design: especially, for purposing stimuli towards specific objectives, such as identifying whether or not a particular brain region is involved in a given task.

We hope that our theoretical framework will enable neuroscientists to state their assumptions more clearly and hence make more confident interpretations of their experimental results. One caveat, however, is that statistical independence tests (and especially, conditional independence tests) are often hard to perform in practice, and require a sufficiently large number of experimental trials.

P105 Detection and evaluation of bursts and rate onsets in terms of novelty and surprise

Junji Ito1, Emanuele Lucrezia1, Guenther Palm2, Sonja Gruen1,3

1Jülich Research Centre, Institute of Neuroscience and Medicine (INM-6), Jülich, Germany; 2University of Ulm, Institute of Neural Information Processing, Ulm, Germany; 3Jülich Research Centre, Institute of Neuroscience and Medicine (INM-10), Jülich, Germany

Correspondence: Junji Ito (j.ito@fz-juelich.de)

BMC Neuroscience 2019, 20(Suppl 1):P105

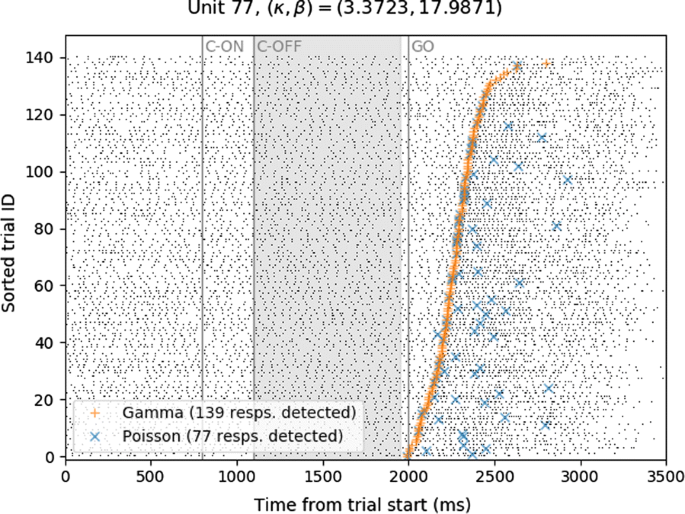
The detection of bursts and also of response onsets is often of relevance in understanding neurophysiological data, but the detection of these events is not a trivial task. Building on a method that was originally designed for burst detection using the so-called burst surprise as a measure [1], we extend it to a significance measure, the strict burst surprise [2, 3]. Briefly, the strict burst surprise is based on a measure called (strict) burst novelty, which is defined for each spike in a spike train as the greatest negative logarithm of the p-values for all ISI sequences ending at the spike. The strict burst surprise is defined as the negative logarithm of the p-value of the cumulative distribution function for the strict burst novelty. The burst detection method based on these measures consists of two stages as follows. In the first stage we model the neuron’s inter-spike interval (ISI) distribution and make an i.i.d. assumption to formulate our null hypothesis. In addition, we define a set of ‘surprising’ events that signify deviations from the null hypothesis in the direction of ‘burstiness’. Here the (strict) burst novelty is used to measure the size of this deviation. In the second stage we determine the significance of this deviation. The (strict) burst surprise is used to measure the significance, since it represents (the negative logarithm of) the significance probability of burst novelty values. We first show how a non-proper choice of null hypothesis affects burst detection performance, and then we apply the method to experimental data from macaque motor cortex [4, 5]. For this application the data are divided into a period for parameter estimation to express a proper null-hypothesis (model of the ISI distribution), and the rest of the data is analyzed by using that null hypothesis. We find that assuming a Poisson process for experimental spike data from motor cortex is rarely a proper null hypothesis, because these data tend to fire more regularly and thus a gamma process is more appropriate. We show that our burst detection method can be used for rate change onset detection (see Fig. 1), because a deviation from the null-hypothesis detected by (strict) burst novelty also covers an increase of firing rate.

Fig. 1

Raster plot of an example single unit (black dots), shown together with rate change onset detection results (orange and blue marks, for gamma and Poisson null hypotheses, respectively). The Poisson null hypothesis fails to detect a lot of rate changes in this case, where the baseline spike train is highly regular (the shape factor k of the spike train is 3.3723, corresponding to a CV of 0.5445)

Full size image

References

1. 1.
   Legendy CR, Salcman M. Bursts and recurrences of bursts in the spike trains of spontaneously active striate cortex neurons. Journal of neurophysiology 1985 Apr 1;53(4):926–39.
2. 2.
   Palm G. Evidence, information, and surprise. Biological Cybernetics 1981 Nov 1;42(1):57–68.
3. 3.
   Palm G. Novelty, information and surprise. Springer Science & Business Media; 2012 Aug 30.
4. 4.
   Riehle A, Wirtssohn S, Grün S, Brochier T. Mapping the spatio-temporal structure of motor cortical LFP and spiking activities during reach-to-grasp movements. Frontiers in neural circuits 2013 Mar 27;7:48.
5. 5.
   Brochier T, Zehl L, Hao Y, et al. Massively parallel recordings in macaque motor cortex during an instructed delayed reach-to-grasp task. Scientific data 2018 Apr 10;5:180055.