28th Annual Computational Neuroscience Meeting: CNS*2019 | BMC Neuroscience | Full Text

28th Annual Computational Neuroscience Meeting: CNS*2019 | BMC Neuroscience | Full Text

O12 Learning where to look: a foveated visuomotor control model

Emmanuel Daucé1, Pierre Albigès2, Laurent Perrinet3

1Aix-Marseille Univ, INS, Marseille, France; 2Aix-Marseille Univ, Neuroschool, Marseille, France; 3CNRS - Aix-Marseille Université, Institut de Neurosciences de la Timone, Marseille, France

Correspondence: Emmanuel Daucé (emmanuel.dauce@centrale-marseille.fr)

BMC Neuroscience 2019, 20(Suppl 1):O12

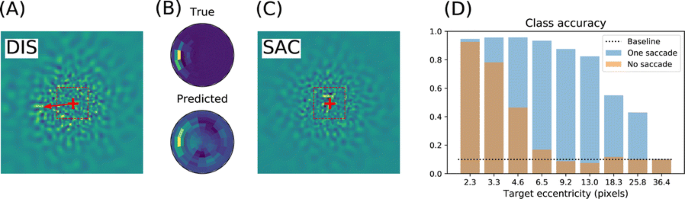
We emulate a model of active vision which aims at finding a visual target whose position and identity are unknown. This generic visual search problem is of broad interest to machine learning, computer vision and robotics, but also to neuroscience, as it speaks to the mechanisms underlying foveation and more generally to low-level attention mechanisms. From a computer vision perspective, the problem is generally addressed by processing the different hypothesis (categories) at all possible spatial configuration through dedicated parallel hardware. The human visual system, however, seems to employ a different strategy, through a combination of a foveated sensor with the capacity of rapidly moving the center of fixation using saccades. Visual processing is done through fast and specialized pathways, one of which mainly conveying information about target position and speed in the peripheral space (the “where” pathway), the other mainly conveying information about the identity of the target (the “what” pathway). The combination of the two pathways is expected to provide most of the useful knowledge about the external visual scene. Still, it is unknown why such a separation exists. Active vision methods provide the ground principles of saccadic exploration, assuming the existence of a generative model from which both the target position and identity can be inferred through active sampling. Taking for granted that (i) the position and category of objects are independent and (ii) the visual sensor is foveated, we consider how to minimize the overall computational cost of finding a target. This justifies the design of two complementary processing pathways: first a classical image classifier, assuming that the gaze is on the object, and second a peripheral processing pathway learning to identify the position of a target in retinotopic coordinates. This framework was tested on a simple task of finding digits in a large, cluttered image (see Fig. 1). Results demonstrate the benefit of specifically learning where to look, and this before actually identifying the target category (with cluttered noise ensuring the category is not readable in the periphery). In the “what” pathway, the accuracy drops to the baseline at mere 5 pixels away from the center of fixation, while issuing a saccade is beneficial in up to 26 pixels around, allowing a much wider covering of the image. The difference between the two distributions forms an “accuracy gain”, that quantifies the benefit of issuing a saccade with respect to a central prior. Until the central classifier is confident, the system should thus perform a saccade to the most likely target position. The different accuracy predictions, such as the ones done in the “what” and the “where” pathway, may also explain more elaborate decision making, such as the inhibition of return. The approach is also energy-efficient as it includes the strong compression rate performed by retina and V1 encoding, which is preserved up to the action selection level. The computational cost of this active inference strategy may thus be way less than that of a brute force framework. This provides evidence of the importance of identifying “putative interesting targets” first and we highlight some possible extensions of our model both in computer vision and modeling.

Fig. 1

Simulated active vision agent: a Example retinotopic input. b Example network output (’Predicted’) compared with ground truth (’True’). c Accuracy estimation after saccade decision. d Orange bars: accuracy of a central classifier w.r.t target eccentricity; Blue bars: classification rate after one saccade (1000 trials average per eccentricity scale)

Full size image

O13 A standardized formalism for voltage-gated ion channel models

Chaitanya Chintaluri1, Bill Podlaski2, Pedro Goncalves3, Jan-Matthis Lueckmann3, Jakob H. Macke3, Tim P. Vogels1

1University of Oxford, Centre for Neural Circuits and Behaviour, Oxford, United Kingdom; 2Champalimaud Center for the Unknown, Lisbon, Portugal; 3Research Center Caesar; Technical University of Munich, Bonn, Germany

Correspondence: Bill Podlaski (william.podlaski@gmail.com)

BMC Neuroscience 2019, 20(Suppl 1):O13

Biophysical neuron modelling has become widespread in neuroscience research, with the combination of diverse ion channel kinetics and morphologies being used to explain various single-neuron properties. However, there is no standard by which ion channel models are constructed, making it very difficult to relate models to each other and to experimental data. The complexity and scale of these models also makes them especially susceptible to problems with reproducibility and reusability, especially when translating between different simulators. To address these issues, we revive the idea of a standardised model for ion channels based on a thermodynamic interpretation of the Hodgkin-Huxley formalism, and apply it to a recently curated database of approximately 2500 published ion channel models (ICGenealogy). We show that a standard formulation fits the steady-state and time-constant curves of nearly all voltage-gated models found in the database, and reproduces responses to voltage-clamp protocols with high fidelity, thus serving as a functional translation of the original models. We further test the correspondence of the standardised models in a realistic physiological setting by simulating the complex spiking behaviour of multi-compartmental single-neuron models in which one or several of the ion channel models are replaced by the corresponding best-fit standardised model. These simulations result in qualitatively similar behaviour, often nearly identical to the original models. Notably, when differences do arise, they likely reflect the fact that many of the models are very finely tuned. Overall, this standard formulation facilitates be er understanding and comparisons among ion channel models, as well as reusability of models through easy functional translation between simulation languages. Additionally, our analysis allows for a direct comparison of models based on parameter settings, and can be used to make new observations about the space of ion channel kinetics across different ion channel subtypes, neuron types and species.

O14 A priori identifiability of a binomial synapse

Camille Gontier1, Jean-Pascal Pfister2

1University of Bern, Department of Physiology, Bern, France; 2University of Bern, Department of Physiology, Bern, Switzerland

Correspondence: Camille Gontier (gontier@pyl.unibe.ch)

BMC Neuroscience 2019, 20(Suppl 1):O14

Synapses are highly stochastic transmission units. A classical model describing this transmission is called the binomial model [1], which assumes that there are N independent release sites, each having the same release probability p; and that each vesicle release gives rise to a quantal current q. The parameters of the binomial model (N, p, q, and the recording noise) can be estimated from postsynaptic responses, either by following a maximum-likelihood approach [2] or by computing the posterior distribution over the parameters [3].

But these estimates might be subject to parameter identifiability issues. This uncertainty of the parameter estimates is usually assessed a posteriori from recorded data, for instance by using re-sampling procedure such as parametric bootstrap.

Here, we propose a methodology for a priori quantifying the structural identifiability of the parameters. A lower bound on the error of parameter estimates can be obtained analytically using the Cramer-Rao bound. Instead of simply assessing a posteriori the validity of their parameter estimates, it is thus possible for experimentalists to select a priori a lower bound on the standard deviation of the estimates and to select the number of data points and to tune the level of noise accordingly.

Besides parameter identifiability, another critical issue is the so-called model identifiability, i.e. the possibility, given a certain number of data points T and a certain level of measurement noise, to find the model of synapse that fits our data the best. For instance, when observing discrete peaks on the histogram of post-synaptic currents, one might be tempted to conclude that the binomial model (“multi-quantal hypothesis”) is the best one to fit the data. However, these peaks might actually be artifacts due to noisy or scarce data points, and data might be best explained by a simpler Gaussian distribution (“uni-quantal hypothesis”).

Model selection tools are classically used to determine a posteriori which model is the best one to fit a data set, but little is known on the a priori possibility (in terms of number of data points or recording noise) to discriminate the binomial model against a simpler distribution.

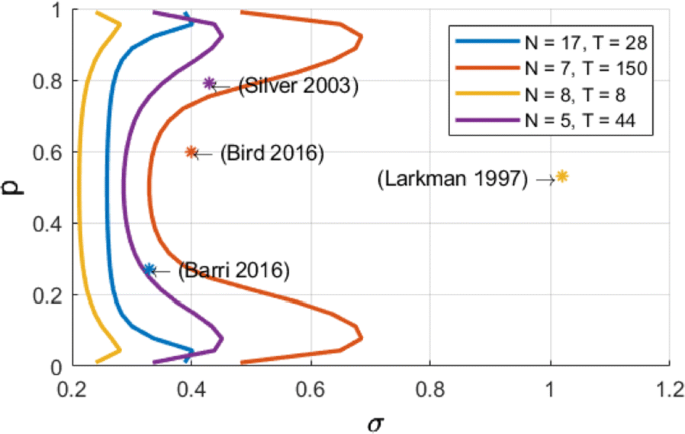
We compute an analytical identifiability domain for which the binomial model is correctly identified (Fig. 1), and we verify it by simulations. Our proposed methodology can be further extended and applied to other models of synaptic transmission, allowing to define and quantitatively assess a priori the experimental conditions to reliably fit the model parameters as well as to test hypotheses on the desired model compared to simpler versions.

Fig. 1

Published estimates of binomial parameters (dots), and corresponding identifiability domains (solid lines: the model is identifiable if, for a given release probability p, the recording noise does not exceed sigma). Applying our analysis to fitted parameters of the binomial model found in previous studies, we find that none of them are in the parameter range that would make the model identifiable

Full size image

In conclusion, our approach aims at providing experimentalists objectives for experimental design on the required number of data points and on the maximally acceptable recording noise. This approach allows to optimize experimental design, draw more robust conclusions on the validity of the parameter estimates, and correctly validate hypotheses on the binomial model.

References

1. 1.
   Katz B. The release of neural transmitter substances. Liverpool University Press (1969): 5–39.
2. 2.
   Barri A, Wang Y, Hansel D, Mongillo G. Quantifying repetitive transmission at chemical synapses: a generative-model approach. eNeuro 2016 Mar;3(2).
3. 3.
   Bird AD, Wall MJ, Richardson MJ. Bayesian inference of synaptic quantal parameters from correlated vesicle release. Frontiers in computational neuroscience 2016 Nov 25; 10:116.

O15 A flexible, fast and systematic method to obtain reduced compartmental models.

Willem Wybo, Walter Senn

University of Bern, Department of Physiology, Bern, Switzerland

Correspondence: Willem Wybo (willem.a.m.wybo@gmail.com)

BMC Neuroscience 2019, 20(Suppl 1):O15

Most input signals received by neurons in the brain impinge on their dendritic trees. Before being transmitted downstream as action potential (AP) output, the dendritic tree performs a variety of computations on these signals that are vital to normal behavioural function [3, 8]. In most modelling studies however, dendrites are omitted due the cost associated with simulating them. Biophysical neuron models can contain thousands of compartments, rendering it infeasible to employ these models in meaningful computational tasks. Thus, to understand the role of dendritic computations in networks of neurons, it is necessary to simplify biophysical neuron models. Previous work has either explored advanced mathematical reduction techniques [6, 10] or has relied on ad-hoc simplifications to reduce compartment numbers [11]. Both of these approaches have inherent difficulties that prevent widespread adoption: advanced mathematical techniques cannot be implemented with standard simulation tools such as NEURON [2] or BRIAN [4], whereas ad-hoc methods are tailored to the problem at hand and generalize poorly. Here, we present an approach that overcomes both of these hurdles: First, our method simply outputs standard compartmental models (Fig 1A). The models can thus be simulated with standard tools. Second, our method is systematic, as the parameters of the reduced compartmental models are optimized with a linear least square fitting procedure to reproduce the impedance matrix of the biophysical model (Fig 1B). This matrix relates input current to voltage, and thus determines the response properties of the neuron [9]. By fitting a reduced model to this matrix, we obtain the response properties of the full model at a vastly reduced computational cost. Furthermore, since we are solving a linear least squares problem, the fitting procedure is well-defined—as there is a single minimum to the error function—and computationally efficient. Our method is not constrained to passive neuron models. By linearizing ion channels around wisely chosen sets of expansion points, we can extend the fitting procedure to yield appropriately rescaled maximal conductances for these ion channels (Fig 1C). With these conductances, voltage and spike output can be predicted accurately (Fig 1D, E). Since our reduced models reproduce the response properties of the biophysical models, non-linear synaptic currents, such as NMDA, are also integrated correctly. Our models thus reproduce dendritic NMDA spikes (Fig 1F). Our method is also flexible, as any dendritic computation (that can be implemented in a biophysical model) can be reproduced by choosing an appropriate set of locations on the morphology at which to fit the impedance matrix. Direction selectivity [1] for instance, can be implemented by fitting a reduced model to a set of locations distributed on a linear branch, whereas independent subunits [5] can be implemented by choosing locations on separate dendritic subtrees. In conclusion, we have created a flexible linear fitting method to reduce non-linear biophysical models. To streamline the process of obtaining these reduced compartmental models, work is underway on a toolbox (https://github.com/WillemWybo/NEAT) that automatizes the impedance matrix calculation and fitting process.

Fig. 1

a Reduction of branch of stellate cell with compartments at 4 locations. b Biophysical (left) and reduced (middle) impedance matrices and error (right) at two holding potentials (top–bottom). c Somatic conductances. d Somatic voltage. e Spike coincidence factor between both models (1: perfect coincidence, 0: no coincidence—4 ms window). F res. g Same as d, but for green resp. blue site

Full size image

References

1. 1.
   Branco T, Clark B, Hausser M. Dendritic discrimination of temporal input sequences in cortical neurons. Science Signaling 2010, Sept:1671–1675.
2. 2.
   Carnevale NT, Hines ML. The NEURON book 2004.
3. 3.
   Cichon J, Gan WB. Branch-specific dendritic Ca2+ spikes cause persistent synaptic plasticity. Nature 2015, 520(7546):180–185.
4. 4.
   Goodman DFM, Brette R. The Brian simulator. Frontiers in neuroscience 2009, 3(2):192– 7.
5. 5.
   Häusser M, Mel B. Dendrites: bug or feature? Current Opinion in Neurobiology 2003, 13(3):372–383.
6. 6.
   Kellems AR, Chaturantabut S, Sorensen DC, Cox SJ. Morphologically accurate reduced order modeling of spiking neurons. Journal of computational neuroscience 2010, 28(3):477–94.
7. 7.
   Koch C, Poggio T. A simple algorithm for solving the cable equation in dendritic trees of arbitrary geometry. Journal of neuroscience methods 1985, 12(4):303–315.
8. 8.
   Takahashi N, Oertner TG, Hegemann P, Larkum ME. Active cortical dendrites modulate perception. Science 2016, 354(6319):1587–90.
9. 9.
   Wybo WA, Torben-Nielsen B, Nevian T, Gewaltig MO. Electrical Compartmentalization in Neurons. Cell Reports 2019, 26(7):1759–1773.e7.
10. 10.
    Wybo WAM, Boccalini D, Torben-Nielsen B, Gewaltig MO. A Sparse Reformulation of the Green’s Function Formalism Allows Efficient Simulations of Morphological Neuron Models. Neural computation 2015, 27(12):2587–622.
11. 11.
    Traub RD, Pais I, Bibbig A, et al. Transient depression of excitatory synapses on interneurons contributes to epileptiform bursts during gamma oscillations in the mouse hippocampal slice. Journal of neurophysiology 2005 Aug;94(2):1225–35.

O16 An exact firing rate model reveals the differential effects of chemical versus electrical synapses in spiking networks

Ernest Montbrió1, Alex Roxin2, Federico Devalle1, Bastian Pietras3, Andreas Daffertshofer3

1Universitat Pompeu Fabra, Department of Information and Communication Technologies, Barcelona, Spain; 2Centre de Recerca Matemàtica, Barcelona, Spain; 3Vrije Universiteit Amsterdam, Behavioral and Movement Sciences, Amsterdam, Netherlands

Correspondence: Alex Roxin (aroxin@crm.cat)

BMC Neuroscience 2019, 20(Suppl 1):O16

Chemical and electrical synapses shape the collective dynamics of neuronal networks. Numerous theoretical studies have investigated how, separately, each of these types of synapses contributes to the generation of neuronal oscillations, but their combined effect is less understood. In part this is due to the impossibility of traditional neuronal firing rate models to include electrical synapses.

Here we perform a comparative analysis of the dynamics of heterogeneous populations of integrate-and-fire neurons with chemical, electrical, and both chemical and electrical coupling. In the thermodynamic limit, we show that the population’s mean-field dynamics is exactly described by a system of two ordinary differential equations for the center and the width of the distribution of membrane potentials —or, equivalently, for the population-mean membrane potential and firing rate. These firing rate equations exactly describe, in a unified framework, the collective dynamics of the ensemble of spiking neurons, and reveal that both chemical and electrical coupling are mediated by the population firing rate. Moreover, while chemical coupling shifts the center of the distribution of membrane potentials, electrical coupling tends to reduce the width of this distribution promoting the emergence of synchronization.

The firing rate equations are highly amenable to analysis, and allow us to obtain exact formulas for all the fixed points and their bifurcations. We find that the phase diagram for networks with instantaneous chemical synapses are characterized by a codimension-two Cusp point, and by the presence of persistent states for strong excitatory coupling. In contrast, phase diagrams for electrically coupled networks is determined by a Takens-Bogdanov codimension-two point, which entails the presence of oscillations and greatly reduces the presence of persistent states. Oscillations arise either via a Saddle-Node-Invariant-Circle bifurcation, or through a supercritical Hopf bifurcation. Near the Hopf bifurcation the frequency of the emerging oscillations coincides with the most likely firing frequency of the network. Only the presence of chemical coupling allows to shift (increase for excitation, and decrease for inhibition) the frequency of these oscillations. Finally, we show that the Takens-Bogdanov bifurcation scenario is generically present in networks with both chemical and electrical coupling.

Acknowledgement: We acknowledge support by the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska Curie grant agreement No. 642563.

O17 Graph-filtered temporal dictionary learning for calcium imaging analysis

Gal Mishne1, Benjamin Scott2, Stephan Thiberge4, Nathan Cermak3, Jackie Schiller3, Carlos Brody4, David W. Tank4, Adam Charles4

1Yale University, Applied Math, New Haven, CT, United States of America; 2Boston University, Boston, United States of America; 3Technion, Haifa, Israel; 4Princeton University, Department of Neuroscience, Princeton, NJ, United States of America

Correspondence: Gal Mishne (gal.mishne@yale.edu)

BMC Neuroscience 2019, 20(Suppl 1):O17

Optical calcium imaging is a versatile imaging modality that permits the recording of neural activity, including single dendrites and spines, deep neural populations using two-photon microscopy, and wide-field recordings of entire cortical surfaces. To utilize calcium imaging, the temporal fluorescence fluctuations of each component (e.g., spines, neurons or brain regions) must be extracted from the full video. Traditional segmentation methods used spatial information to extract regions of interest (ROIs), and then projected the data onto the ROIs to calculate the time-traces [1]. Current methods typically use a combination of both a-priori spatial and temporal statistics to isolate each fluorescing source in the data, along with the corresponding time-traces [2, 3]. Such methods often rely on strong spatial regularization and temporal priors that can bias time-trace estimation and that do not translate well across imaging scales.

We propose to instead model how the time-traces generate the data, using only weak spatial information to relate per-pixel generative models across a field-of-view. Our method, based on spatially-filtered Laplacian-scale mixture models [4,5], introduces a novel non-local spatial smoothing and additional regularization to the dictionary learning framework, where the learned dictionary consists of the fluorescing components’ time-traces.

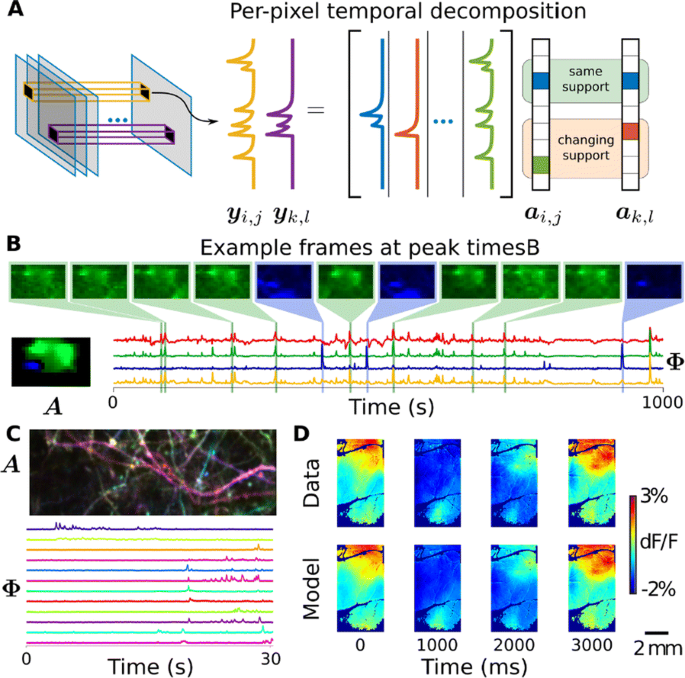
We demonstrate on synthetic and real calcium imaging data at different scales that our solution has advantages regarding initialization, implicitly inferring number of neurons and simultaneously detecting different neuronal types (Fig. 1). For population data, we compare our method to a current state-of-the-art algorithm, Suite2p, on the publicly available Neurofinder dataset (Fig. 1C). The lack of strong spatial contiguity constraints allows our model to isolate both disconnected portions of the same neuron, as well as small components that would otherwise be over-shadowed by larger components. In the latter case, this is important as such configurations can easily cause false transients which can be scientifically misleading. On dendritic data our method isolates spines and dendritic firing modes (Fig. 1D). Finally, our method can partition widefield data [6] in to a small number of components that capture the scientifically relevant neural activity (Fig. 1E-F).

Fig. 1

a Our method uses a per-pixel generative model with non-local spatially correlated coefficients. b Temporal DL finds subtle features in the Neurofinder dataset. For example, shown here is an apical dendrite (blue) significantly overlapping with a soma (green) was isolated. Manually labeled soma (yellow) and Suite2p (red) do not account for the apical, resulting in contaminated time-traces. c Applications to dendritic data extracts both dendrite and spine activity (bottom), as seen by the spatial maps where each component is colored differently (top). d In widefield imaging, the reconstructed movie recapitulates the behaviorally-triggered dynamics [6], demonstrating that it captures the scientifically-relevant activity

Full size image

Acknowledgments: M is supported by NIH NIBIB and NINDS (grant R01EB026936).

References

1. 1.
   Mukamel EA, Nimmerjahn A, Schnitzer MJ. Automated analysis of cellular signals from large-scale calcium imaging data. Neuron 2009, 63, 747–760.
2. 2.
   Pachitariu M, et al. Suite2p: beyond 10,000 neurons with standard two-photon microscopy. bioRxiv, 2016. 061507
3. 3.
   Pnevmatikakis EA, et al. Simultaneous denoising, deconvolution, and demixing of calcium imaging data. Neuron 2016, 89, 285–299.
4. 4.
   Garrigues P, Olshausen BA. Group sparse coding with a laplacian scale mixture prior. NIPS 2010, 676–684.
5. 5.
   Charles AS, Rozell CJ. Spectral superresolution of hyperspectral imagery using reweighted l1 spatial filtering. IEEE Geosci. Remote Sens. Lett. 2014, 11, 602–606.
6. 6.
   Scott BB, et al. Imaging Cortical Dynamics in GCaMP Transgenic Rats with a Head-Mounted Widefield Macroscope, Neuron 2018, 100, 1045–1058.

O18 Drift-resistant, real-time spike sorting based on anatomical similarity for high channel-count silicon probes

James Jun1, Jeremy Magland1, Catalin Mitelut2, Alex Barnett1

1Flatiron Institute, Center for Computational Mathematics, New York, NJ, United States of America; 2Columbia University, Department of Statistics, New York, United States of America

Correspondence: James Jun (jjun@flatironinstitute.org)

BMC Neuroscience 2019, 20(Suppl 1):O18

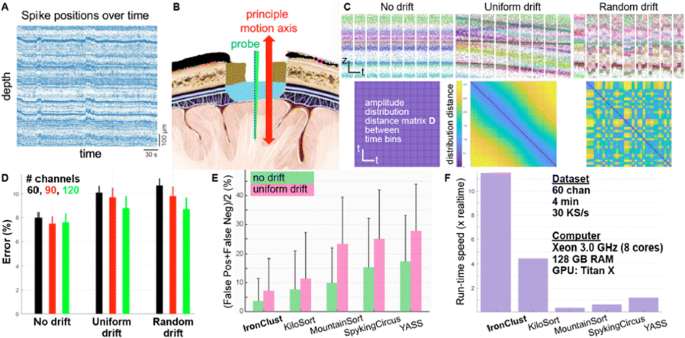
Extracellular electrophysiology records a mixture of neural population activity at a single spike resolution. In order to resolve individual cellular activities, a spike-sorting operation groups together similar spike waveforms distributed at a subset of electrodes adjacent to each neuron. Penetrating micro-electrode arrays are widely used to measure the spiking activities from behaving animals, but silicon probes can be drifted in the brain due to animal movements or tissue relaxation following a probe penetration. The probe drift issue results in errors in conventional spike sorting operations that assumes stationarity in spike waveforms and amplitudes. Some of the latest silicon probes [1] offer a whole-shank coverage of closely-spaced electrode arrays, which can continually capture the spikes generated by neurons moving along the probe axis. We introduce a drift-resistant spike sorting algorithm for high channel-count, high-density silicon probe, which is designed to handle gradual and rapid random probe movements. IronClust takes advantage of the fact that a drifting probe revisits the same anatomical locations at various times. We apply a density-based clustering by grouping a temporal subset of the spiking events where the probe occupied similar anatomical locations. Anatomical similarities between a disjoint set of time bins are determined by calculating the activity histograms, which capture the spatial structures in the spike amplitude distribution based on the peak spike amplitudes on each electrode. For each spiking event, the clustering algorithm (DPCLUS [2]) computes the distances to a subset of its neighbors selected by their peak channel locations and the anatomical similarity. Based on the k-nearest neighbors [3], the clustering algorithm finds the density peaks based on the local density values and the nearest distances to the higher-density neighbors, and recursively propagates the cluster memberships toward a decreasing density gradient, The accuracy of our algorithm was evaluated using validation datasets generated using a biophysically detailed neural network simulator (BioNet [4]), which generated three scenarios including stationary, slow monotonic drift, and fast random drift cases. IronClust achieved ~8% error on the stationary dataset, and ~10% error on the gradual or random drift datasets, which significantly outperformed existing algorithms (Fig. 1). We also found that additional columns of electrodes improve the sorting accuracy in all cases. IronClust achieved over 11x of the real-time speed using GPU, and over twice faster than other leading algorithm. In conclusion, we realized an accurate and scalable spike sorting operation resistant to probe drift by taking advantage of an anatomically-aware clustering and parallel computing.

Fig. 1

a Probe drift causes coherent shifts in the spike positions preserving the anatomical structure. b Principal probe movement occurs along the probe axis. c Three drift scenarios and the anatomical similarity matrices between time bins. d Clustering errors for various drift scenarios and electrode layouts. e Accuracy comparison. f Speed comparison between multiple sorters

Full size image

References

1. 1.
   Jun JJ et al. Fully integrated silicon probes for high-density recording of neural activity. Nature 2017 Nov;551(7679):232.
2. 2.
   Rodriguez A, Laio A. Clustering by fast search and find of density peaks. Science 2014 Jun 27;344(6191):1492–6.
3. 3.
   Rodriguez A, d’Errico M, Facco E, Laio A. Computing the free energy without collective variables. Journal of chemical theory and computation 2018 Feb 5;14(3):1206–15.
4. 4.
   Gratiy SL, et al. BioNet: A Python interface to NEURON for modeling large-scale networks. PloS one 2018 Aug 2;13(8):e0201630.

P1 Promoting community processes and actions to make neuroscience FAIR

Malin Sandström, Mathew Abrams

INCF, INCF Secretariat, Stockholm, Sweden

Correspondence: Malin Sandström (malin.sandstrom@incf.org)

BMC Neuroscience 2019, 20(Suppl 1):P1

The FAIR data principles were established as a general framework to facilitate knowledge discovery in research. Since the FAIR data principles are only guidelines, it is up to each domain to establish the standards and best practices (SBPs) that fulfill the principles. Thus, INCF is working with the community to develop, endorse, and adopt SBPs in neuroscience.

Develop: Connecting communities to support FAIR(er) practices

INCF provides 3 forums in which community members can come together to develop SBPs: Special Interest Groups (SIGs), Working Groups (WGs), and the INCF Assembly. SIGs are composed of a group of community members with the same interest, who gather and self-organize around tools, data, and community needs in a specific area. The SIGs will also serve as the focus for getting agreement and community buy-in on the use of these standards and best practices. INCF WGs are extensions of SIGs that receive funding from INCF to develop or extend existing SBPs, for example to support additional data types, or the development of a new SBP. The WG plan must include a plan for gathering appropriate input from the membership and the community. for example to support additional data types, or the development of a new SBP.

Endorse: Formalized standards endorsement process

The endorsement process is a continuous loop of feedback from the committee and the community to the developer(s) of the SBPs (e.g. PyNN and NeuroML [1,2]). Developers submit their SBPs for endorsement to the INCF SBP Committee who in turn vets the merit of the SBPs and publishes a report on the proposed standard covering openness, FAIRness, testing and implementation, governance, adoption and use, stability, and support. Then community is invited to comment during a 60-day period before the committee takes the final decision. Endorsed SBPs are then made available on incf.org and promoted to the community, to journals, and to funders through INCF’s training and outreach efforts.

Promote Adoption: Outreach and training

To promote adoption, INCF offers the yearly INCF Assembly where SIGs and WGs can present their work and engage the wider community. Training materials are also integrated into the INCF TrainingSpace, a platform linking world-class neuroinformatics training resources, developed by INCF in collaboration with its partners, and existing community resources. In addition to outreach and training, INCF also developed KnowledgeSpace, a community-based encyclopedia for neuroscience that links brain research concepts to the data, models, and literature that supports them, demonstrating how SBPs can facilitate linking brain research concepts with data, models and literature from around the world. It is an open project and welcomes participation and contributions from members of the global research community. KS is the result of recommendations from a community workshop held by the INCF Program on Ontologies of Neural Structures in 2012.

References

1. 1.
   Martone M, Das S, Goscinski W, et al. Call for community review of NeuroML — A Model Description Language for Computational Neuroscience [version 1; not peer reviewed] F1000Research 2019, 8:75 (document) (https://doi.org/10.7490/f1000research.1116398.1).
2. 2.
   Martone M, Das S, Goscinski W, et al. Call for community review of PyNN — A simulator-independent language for building neuronal network models [version 1; not peer reviewed]. F1000Research 2019, 8:74 (document) (https://doi.org/10.7490/f1000research.1116399.1).

P2 Ring integrator model of the head direction cells

Anu Aggarwal

Grand Valley State University, Electrical and Computer Engineering, Grand Rapids, MI, United States of America

Correspondence: Anu Aggarwal (aaagganu@gmail.com)

BMC Neuroscience 2019, 20(Suppl 1):P2

Head direction (HD) cells have been demonstrated in the post subiculum [1, 2] of the hippocampal formation of the brain. Ensembles of the HD cells provide information about heading direction during spatial navigation. An Attractor Dynamic model [3] has been proposed to explain the unique firing patterns of the head direction cells. Here, we present a novel Ring Integrator model of the HD cells. This model is an improvement over the Attractor Dynamic model as it achieves the same functionality with fewer neurons and explains how the HD cells align to orienting cues.

References

1. 1.
   Taube JS, Muller RU, Ranck JB. Head-direction cells recorded from the postsubiculum in freely moving rats. I. Description and quantitative analysis. Journal of Neuroscience 1990 Feb 1;10(2):420–35.
2. 2.
   Taube JS, Muller RU, Ranck JB. Head-direction cells recorded from the postsubiculum in freely moving rats. II. Effects of environmental manipulations. Journal of Neuroscience 1990 Feb 1;10(2):436–47.
3. 3.
   McNaughton BL, Battaglia FP, Jensen O, Moser EI, Moser MB. Path integration and the neural basis of the ‘cognitive map’. Nature Reviews Neuroscience 2006 Aug;7(8):663.

P3 Parametric modulation of distractor filtering in visuospatial working memory.

Davd Bestue1, Albert Compte2, Torkel Klingberg3, Rita Almeida4

1IDIBAPS, Barcelona, Spain; 2IDIBAPS, Systems Neuroscience, Barcelona, Spain; 3Karolinksa Institutet, Stockholm, Sweden; 4Stockholm University, Stockholm, Sweden

Correspondence: Davd Bestue (davidsanchezbestue@hotmail.com)

BMC Neuroscience 2019, 20(Suppl 1):P3

Although distractor filtering has been long identified as a fundamental mechanism to achieve an efficient management of working memory, there are not many tasks where distractors are parametrically modulated both in the temporal and the similarity domain simultaneously. Here, 21 subjects participated in a visuospatial working memory task (vsWM) where distractors could be presented prospectively or retrospectively at two different delay times (200 and 7000 ms). Moreover, distractors were presented close or far away from the target. As expected, changes in the temporal and the similarity domain induced different distraction behaviours. In the similarity domain, we observed that close-by distractors induced an attractive bias while far distractors induced a repulsive one. Interestingly, this pattern of biases occurred both for prospective and retrospective distractors, suggesting common mechanisms of interference with the behaviorally relevant target. This result is in line with a previously validated bump-attractor model where diffusing bumps of neural activity attract or repel each other in the delay period [1]. In the temporal domain, we found a stronger effect for prospective distractors and short delays (200ms). Intriguingly, we observed that a retrospective distractor at 7000 ms also affected behavior, suggesting that irrelevant distractor memory traces can last longer than previously considered in computational models. One possibility is that persistent-activity based mechanisms underpin target storage while synaptic-based mechanisms underlie distractor memory traces. To gather support for this idea, we ran the same experiment with a 3T fMRI in 6 participants. Based on previous studies where sensory areas were not resistant to distractors [2], we hypothesized that sensory areas would represent all visual stimuli while associative areas like IPS would subserve memory-for-target function. Importantly, the synaptic hypothesis for distractor storage would predict that despite the behavioral evidence for retrospective distractor memory in this task, retrospective distractors would not be represented in the activity of either area, despite strong representations of the target. To test this, we will map parametric behavioral outputs into physiological activity readouts [3] for the different distractor conditions and we will explore the biological mechanism of distractor storage in working memory by comparing distractor storage in the retrospective 7000 ms condition with target storage in the absence of distractors. All together, these results open the door to an integrative model of working memory where different neural mechanisms and multiple brain regions are taken into account.

References

1. 1.
   Almeida R, Barbosa J, Compte A. Neural circuit basis of visuo-spatial working memory precision: a computational and behavioral study. Journal of Neurophysiology 2015 Jul 15;114(3):1806–18.
2. 2.
   Bettencourt KC, Xu Y. Decoding the content of visual short-term memory under distraction in occipital and parietal areas. Nature Neuroscience 2016 Jan;19(1):150.
3. 3.
   Ester EF, Sprague TC, Serences JT. Parietal and frontal cortex encode stimulus-specific mnemonic representations during visual working memory. Neuron 2015 Aug 19;87(4):893–905.

P4 Dynamical phase transitions study in simulations of finite neurons network

Cecilia Romaro1, Fernando Najman2, Morgan Andre2

1University of São Paulo, Department of Physics, Ribeirão Preto, Brazil; 2University of São Paulo, Institute of Mathematics and Statistics, São Paulo, Brazil

Correspondence: Cecilia Romaro (cecilia.romaro@usp.br)

BMC Neuroscience 2019, 20(Suppl 1):P4

In [1], Ferrari et al. introduced a continuous time model for network of spiking neurons with binary membrane potential. It consists in an infinite system of interacting point processes. Each neuron in the one-dimensional lattice Z has two post-synaptic neurons, which are its two immediate neighbors. There is only two possible states for a given neuron, which are “active” or “quiescent” (1 or 0), and the neuron goes from “active” to “quiescent” either when it spikes, either when it is affected by the leakage effect, it goes from 0 to 1 when one of its presynaptic neurons spikes. For a given neuron the spikes are modeled as the events of a Poisson process of parameter 1, while the leakage events are modeled as the events of a Poisson process of some positive parameter gamma γ, all the processes being mutually independents. It was shown that this model presents a phase transition with respect to the parameter γ. This means that there exists a critical value for the parameter γ, denoted γc, such that, when γ>γc all neurons will once for all end up in the “quiescent” state with probability one; and when γ<γc there is a positive probability that the neurons will come back to the “active” state infinitely often.

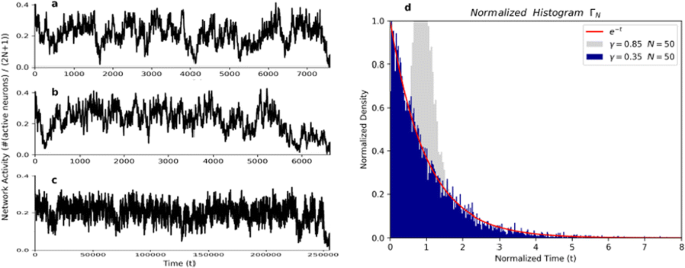
However, when modeling the brain, it is usual to work with a necessarily finite number of neurons. Thus, we consider a finite version of the infinite system: instead of a process defined on entire lattice Z, we consider a version of the process defined on the finite window {−N, −N + 1, …, N − 1 N} (the number of neurons is therefore 2N + 1). When the number of neurons is finite we know by elementary results about Markov chains that the absorbent state, where all neurons are “quiescent”, will necessarily be reached in some finite time for any value of γ. The time t spent to reach the absorbent state depends on the network number of neuron 2N + 1 and the arbitrary parameter γ. For example, around 107 random numbers were picked up until the network reached the absorbent state for N = 100 and γ = 0.375, but around 109 random numbers were required when N was increased to 500 (Fig. 1).

Fig. 1

The activity of network with (a and b) N = 100 or c N = 500 and γ = 0.375. Around 107 (a and b and 109) c random numbers were required until the network reaches the absorbent state. d Histogram normalized of the time t of extinction for N = 50 and gamma = 0.35 for 10,000 turns compared with the function exp(−t) in red

Full size image

So, we conjecture that, for a γ less than the critical gamma γc, the finite model presents a dynamical phase transition, as first defined in [2]. By this we mean that for a finite number of neurons, the distribution of the time of extinction (T(N,γ)) re-normalized (divided by its expectation) converges in distribution to an exponential random variable of parameter 1 when the number of neurons grows (N→∞). To back up our conjecture we build up the present model in python and run it 10,000 turns for N = (10, 50, 100, 500, 1000), J = (0.40, 0.35, 0.30) and plot the normalized histogram. The Fig. 1d shows the normalized histogram of the time of extinction for N = 50 (101 neurons) and J = 0.35 for 10,000 simulations and the function e-t in red.

Acknowledgements: This work was produced as part of the activities of FAPESP Research, Disseminations and Innovation Center for Neuromathematics (Grant 2013/07699-0, S. Paulo Research Foundation).

References

1. 1.
   Ferrari PA, Galves A, Grigorescu I, Löcherbach E. Phase transition for infinite systems of spiking neurons. Journal of Statistical Physics 2018 Sep 1;172(6):1564–75.
2. 2.
   Cassandro M, Galves A, Picco P. Dynamical phase transitions in disordered systems: the study of a random walk model. In Annales de l’IHP Physique théorique 1991 (Vol. 55, No. 2, pp. 689–705).